Eyeballing recept vaše očne jabučice: BME60B projekt: 9 koraka

2024 Autor: John Day | [email protected]. Zadnja promjena: 2024-01-30 09:32

Napisali: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Povećanje je jedna od ključnih značajki prisutnih naočala za čitanje, koje su klasificirane prema recepturi dioptrije. Prema Tehničkom sveučilištu Michigan, dioptrija je žarišna duljina leće, obično se mjeri u mm, u jedinici metara (Michigan Technology University). Budući da naočale za čitanje imaju konveksne leće, žarišna duljina bi bila pozitivna, što bi uzrokovalo i pozitivnu dioptriju (HyperPhysics). Žarišna duljina se povećava kako se udaljenost između objekta sve više udaljava od stvarne leće, a to dovodi do smanjenja dioptrije jer su obrnuto proporcionalne. Stoga bi naočale za čitanje s dodatnom dioptrijom pomogle leći da zumira prikaz tako da se može činiti da je žarišna duljina manja povećanjem vrijednosti dioptrije.

Predstavljeni kod će se koristiti za predviđanje dioptrije leće s nepoznatim receptom. Za unos recepta koriste se dva ulaza: fotografija kontrolirane pozadine bez upotrebe leća i još jedna fotografija iste pozadine, ali kroz leću po izboru. Program će mjeriti izobličenja između ove dvije fotografije. Odatle ćemo moći procijeniti dioptriju leće i proizvesti rezultat koji će korisnik moći vidjeti.

Za ovaj Instructable trebat će vam:

• Crno-bijeli uzorak šahovske ploče otisnut na listu papira dimenzija 11x8,5
• Kamera s mogućnošću zaključavanja fokusa
• Stativ ili nešto slično za pričvršćivanje fotoaparata
• Razni recepti za naočale za čitanje
• MATLAB

Korak 1: Snimite fotografije

Da biste izračunali povećanje leće, morate je moći usporediti sa stvarnom veličinom objekta. Za ovaj projekt uspoređivat ćemo uvećanu sliku s kontrolnom slikom.

Dakle, prvi korak je snimiti dvije fotografije iste slike - prvu samo kamerom, a drugu kroz leće naočala za čitanje koje želite testirati.

Snimit ćete crno -bijelu šahovnicu dimenzija 8,5 x 11 inča s rešetkom od 1 inča. Postavite kameru 11 inča od šahovnice. Prije snimanja fotografija, fokus fokusirajte na šahovnicu.

Fotografirajte šahovnicu bez naočala za čitanje. Zatim, ne pomičući ništa, stavite naočale za čitanje ispred kamere i snimite drugu fotografiju.

Pazite da se položaj vaše kamere ne pomiče između snimaka. Jedino što bi se trebalo promijeniti između dvije fotografije je prisutnost leća naočala ispred kamere.

Kad završite s fotografijama, prenesite ih na računalo.

Korak 2: Umetnite slike u MATLAB

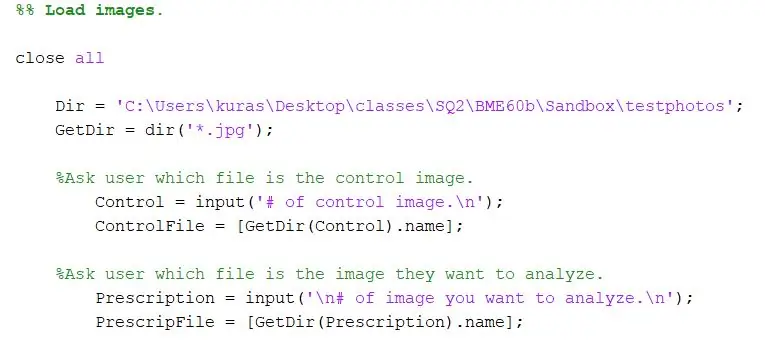
Otvorite novu skriptu.

Prvo odredite direktorij u kojem su fotografije pohranjene. Zatim upotrijebite funkciju dir za izdvajanje-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Za naš projekt željeli smo obavijestiti korisnika programa koje datoteke želi usporediti. Prvi odjeljak traži od korisnika da navede kontrolnu sliku, a drugi traži od korisnika da navede testnu sliku.

• %Pitajte korisnika koja je datoteka kontrolna slika.
• Control = input ('# kontrolne slike. / N');
• ControlFile = [GetDir (Control).name]
• %Pitajte korisnika koju datoteku želi analizirati.
• ChooseFile = input ('\ n# slike koju želite analizirati. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Korak 3: Analiza slike

Slika u boji u MATLAB -u je veličine MxNx3, dok je slika u sivim tonovima MxN. To znači da je brže poboljšati/urediti sliku u sivim tonovima jer ima manje podataka za praćenje. Koristite rgb2gray za pretvaranje slike u sive. (Funkcija imrotate korištena je jer su naše fotografije bile vodoravne - ovaj redak koda može, ali i ne mora biti potreban u vašoj verziji.)

• %pretvoriti u sive i rotirati
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotirati (I, 90);

Zatim prikažite sliku. Funkcija podcrtavanja koristi se tako da se testna slika može nalaziti pored kontrole u kasnijim koracima.

• %prikaz
• slika (1);
• podcrt (1, 2, 1)
• imshow (I);
• naslov (ControlFile);

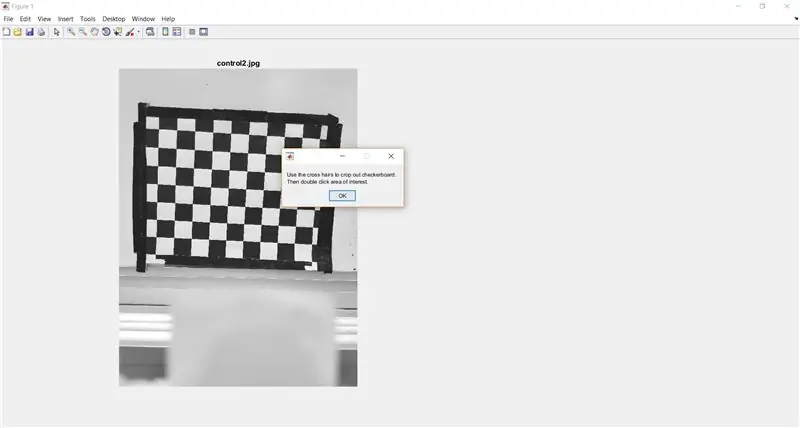
Upotrijebite imcrop da biste zatražili od korisnika da izreže šahovnicu s cijele slike. Sljedeći kôd također prikazuje okvir s porukom koji daje upute korisniku.

• %izrezati šahovnicu za analizu
• waitfor (msgbox ({'Upotrijebite križance za izrezivanje šahovske ploče.', 'Zatim dvaput kliknite područje interesa.'}));
• I_crop = imcrop (I);

Za binarnu sliku upotrijebite imbinarize.

I_binary = imbinarize (I_crop);

Korak 4: Izračunajte širinu bijelih kvadrata na šahovnici

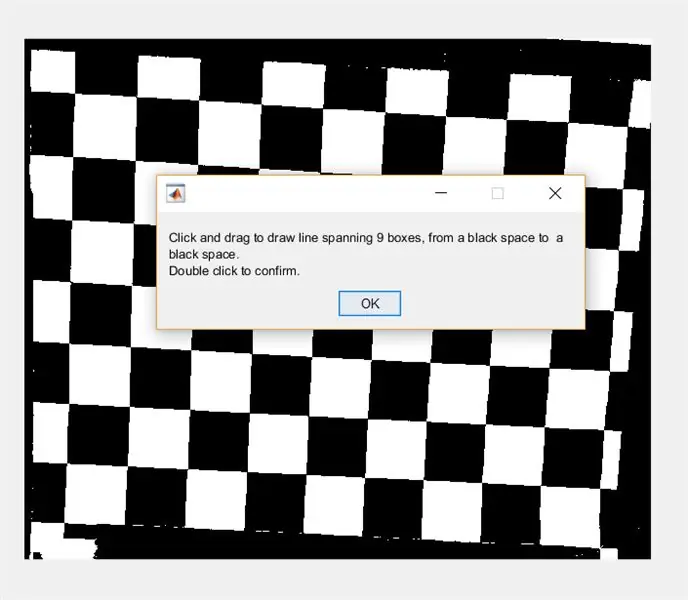
Zatim zamolite korisnika da nacrta liniju preko slike pomoću imline. Ova linija trebala bi se protezati vodoravno preko šahovske ploče. Trebao bi početi i završiti na crnom kvadratu (nije važno gdje)- to je zato što ćemo mjeriti širinu bijelih kvadrata, a ne crne.

• %linija izvlačenja
• slika (1)
• podcrt (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Kliknite i povucite da biste nacrtali liniju koja obuhvaća 9 okvira, od razmaka do razmaka.', 'Dvaput kliknite za potvrdu.'}));
• linija = imline;
• položaj = čekanje (red);
• krajnje točke = line.getPosition;

Izdvojite X i Y koordinate za krajnje točke povučene crte.

• X = krajnje točke (:, 1)
• Y = krajnje točke (:, 2);

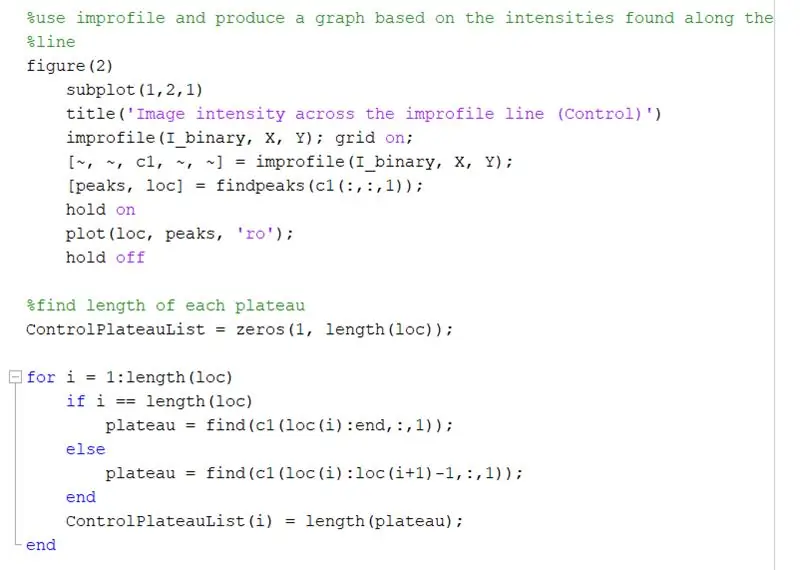
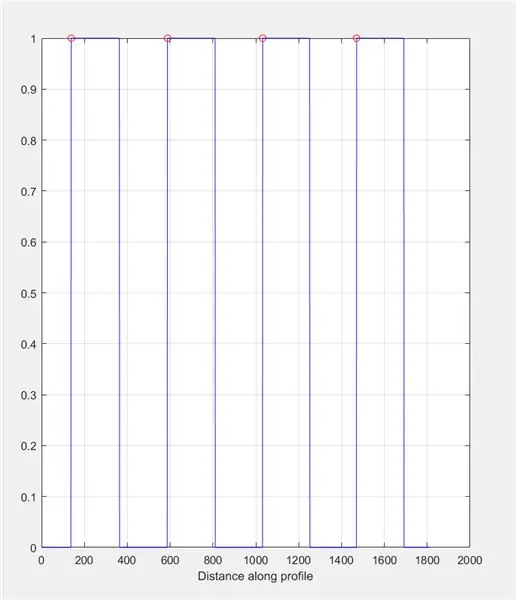
Upotrijebite improfile za izradu grafikona na temelju intenziteta koji se nalaze duž nacrtane crte. Ovo bi trebalo nalikovati kvadratnom valu u rasponu od 0 (crno) do 1 (bijelo). Izračunajte vrhove i njihovo mjesto.

• slika (2)
• podcrt (1, 2, 1)
• title ('Intenzitet slike preko improvizirane linije (kontrola)')
• improfile (I_binary, X, Y); mreža uključena;
• [~, ~, c1, ~, ~] = neprovjerena (I_binarna, X, Y);
• [piaks, loc] = findpeaks (c1 (:,:, 1));
• drži se
• zaplet (loc, vrhovi, 'ro');
• odgađati

Odredite duljinu svakog platoa na improviziranom grafikonu pomoću for petlje. Pokrenite for petlju za istu količinu vrhova koliko postoji na grafikonu neprovjerene datoteke. Za izračun duljine svakog platoa upotrijebite funkciju "pronađi" da pronađete sve lokacije na kojima postoji vrijednost "1" umjesto vrijednosti "0". Zatim izračunajte duljinu tog niza kako biste dobili ukupnu duljinu platoa, koja bi trebala biti jednaka širini bijelog kvadrata u pikselima. ControlPlateauList = nule (1, dužina (loc));

za i = 1: duljina (loc)

ako je i == duljina (loc)

plato = pronaći (c1 (loc (i): kraj,:, 1));

drugo

plato = pronaći (c1 (loc (i): loc (i+1) -1,:, 1));

kraj

ControlPlateauList (i) = duljina (plato);

kraj

Korak 5: Ponovite korake 3 i 4 za probnu sliku

*Napomena: kada crtate improviziranu liniju na probnoj slici, svakako je nacrtajte preko kvadrata koji odgovaraju liniji koju ste nacrtali na kontrolnoj slici.

Korak 6: Izračunajte povećanje objektiva

Uvećana mjerenja izračunavaju se dijeljenjem srednje vrijednosti duljine platoa, koja je izračunata u koraku 5, sa srednjom dužinom kontrolnog platoa, koja je izračunata u koraku 4. To se računa na 1,0884.

povećanje = srednja vrijednost (platoList)/srednja vrijednost (ControlPlateauList);

Korak 7: Pronalaženje R-kvadrata i korisnički recept putem interpolacije

Koristeći kôd:

• md1 = fitlm (S obzirom na recept, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Možemo pronaći vrijednost R-kvadrata grafikona GivenPresciption (naše leće daju vrijednosti) u odnosu na MagArray (niz omjera mjerenja povećanja koje smo izračunali ranije). Imajući dovoljno visoku vrijednost R-kvadrata, može se zaključiti da postoji dovoljno jaka korelacija koja opravdava uporabu ove metode. U ovom konkretnom slučaju vrijednost R-kvadrata bila je 0,9912, što sugerira snažnu korelaciju i stoga je opravdano koristiti ovu metodu u analizi.

Pomoću funkcije:

Recept = interp1 (MagArray, GivenPrescription, povećanje, 'linearno');

Možemo interpolirati odgovarajuću propisanu vrijednost (na osi x) našeg omjera povećanja (vrijednost na osi y) i pronaći koji je korisnički recept.

Interpoliranje podataka važno je za funkcioniranje ove metode jer nam omogućuje da na temelju informacija koje imamo donosimo pretpostavke o informacijama koje nemamo. Iako bi linija koja najbolje pristaje tehnički bila jači kandidat za ovu pretpostavku, stvaranje granica za smanjenje broja izlaza ima isti učinak kao što dioptrijske naočale u svakom slučaju dolaze u postupno ujednačenim vrijednostima. To se objašnjava u kasnijim koracima.

Korak 8: Prikaz korisničkog recepta na grafikonu

Koristeći sljedeći kôd:

• lik;
• zaplet (DatePrescription, MagArray, '-g')
• drži se
• zaplet (recept, povećanje, 'bp')
• odgađati
• rešetka
• legenda ('Podaci', 'Interpolirane točke', 'Lokacija', 'SZ')

Možemo nacrtati grafikon koji prikazuje omjere povećanja u odnosu na zadani recept sa zelenom linijom i pronađene podatke našeg izračunatog povećanja u odnosu na naš interpolirani recept sa plavom zvjezdicom. Zatim legenda označava naslov, x-os i y-os te postavlja legendu u gornji lijevi kut.

Korak 9: Suzite recept

Sljedeći kôd koristi se za zaokruživanje recepta:

• ako je recept <= 1.125

  CalculatedPrescription = '1.0';

• inače ako je recept <= 1.375

  CalculatedPrescription = '1,25';

• inače ako je recept <= 1.625

  CalculatedPrescription = '1.5';

• inače ako je recept <= 1.875

  CalculatedPrescription = '1.75';

• inače ako je recept <= 2,25

  CalculatedPrescription = '2.0';

• inače ako je recept <= 2.625

  CalculatedPrescription = '2.5';

• inače recept <= 3

  CalculatedPrescription = '2.75';

• inače ako je recept <= 3.375

  CalculatedPrescription = '3.25';

• drugo

  CalculatedPrescription = 'nepoznato';

• kraj

Recept pronađen interpolacijom ne odražava nužno stvarni recept - to je zato što će uvijek doći do malih razlika u analizi fotografije zbog ljudske pogreške. Stoga nam je ovaj korak potreban za klasifikaciju stvarnog recepta.

Recepti koji se daju obično počinju od 1,0 dioptrije i povećavaju se za, 25 u svojim receptima, pa nakon izračuna recepta želimo odrediti recept koji najbolje odgovara onome što bi korisniku moglo zatrebati. Nakon izračuna recepta, vodimo ga kroz navedene naredbe If kako bismo provjerili njegovu vrijednost i odredili koji je recept potreban. Sve što je manje ili jednako 1,125, tada je recept 1,0. Sve što je manje ili jednako 1,375, recept je 1,25. Sve što je manje ili jednako 1,625, recept je 1,5. Sve što je manje ili jednako 1,845, recept je 1,75. I tako dalje.

Vrijednosti se povećavaju jer provjeravamo jesu li vrijednosti manje od. Ako bismo smanjili vrijednosti, tada bi prva naredba if čitala prvu if naredbu cijelo vrijeme. Ako je recept najmanji, želimo da ga odmah prepozna kao najmanji, pa je zato najmanja vrijednost ono s čime smo počeli. Sve što je veće od najveće vrijednosti znači da recept nije u rasponu s našim podacima, pa će dati niz "Nepoznato".