Znate li o podešavanju ESP32 ADC -a?: 29 koraka

2024 Autor: John Day | [email protected]. Zadnja promjena: 2024-01-30 09:35

Danas ću govoriti o jednom tehničkom pitanju, ali mislim da bi svi koji rade s ESP32 trebali znati: pitanje prilagodbe čitanja ADC-a (analogno-digitalni pretvarač). Smatram da je to važno jer kada radite "mjerenje", posebno s instrumentom koji ima analogni izlaz, morate biti potpuno sigurni da se očitanje izvodi ispravno.

U današnjem videu stoga ćemo provoditi mjerenja pomoću "analogno-digitalnog pretvarača" ESP32, promatrati odstupanja pretvorbe i primijeniti metodu podešavanja / kalibracije ADC-a.

Korak 1: Što je AD Converter?

AD pretvarač je sklop sposoban prevesti analognu (kontinuiranu) veličinu u digitalne (diskretne) vrijednosti. Što to znači? To znači da iako digitalne vrijednosti mogu pretpostaviti samo diskretne vrijednosti nastale kombinacijom nula i jedinica, analogna veličina može poprimiti bilo koju vrijednost unutar raspona. Na primjer, ako bismo izmjerili napon idealne AA ćelije, mogli bismo pronaći bilo koju vrijednost između 0V i 1.5V, budući da je to analogna veličina. Izlazno stanje idealne svjetiljke mora poprimiti samo dva stanja (isključeno ili uključeno), što je diskretna veličina. Budući da mikrokontroleri rade pomoću ove diskretne logike, potreban nam je sklop sposoban za prevođenje analogne veličine u digitalnu (ili diskretnu).

Korak 2: Korišteni resursi

• Jedna kartica Lolin32 Lite v1.0.0

• Tektronix TDS1001C osciloskop za snimanje

• Jedan USB kabel za ESP32

• Hantek DSO4102C osciloskop kao generator signala

Korak 3: ESP32 ADC

Prema podacima Espressifa, ESP32 čipovi mogu imati +/- 6% razlike od jednog do drugog čipa u izmjerenim rezultatima.

Osim toga, pretvorba NEMA linearni odgovor za svaki raspon za čitanje. Espressif nudi metodu kalibracije i predlaže korisnicima da primijene druge metode ako smatraju da je potrebno postići željenu točnost.

Izvršit ćemo prikupljanje podataka, a zatim ćemo pokazati odgovore ADC -a i primjer primjene matematičkog procesa za čitanje prilagodbe.

Postoji nekoliko (jednostavnijih ili složenijih) načina za postizanje ovih popravaka. Na vama je da ocijenite najprikladnije za vaš projekt.

Ova prikazana ovdje će imati ilustrativnu svrhu i pokušat će se pozabaviti zanimljivim točkama koje se mogu uočiti tijekom prilagodbi.

Korak 4: Korišteni krug

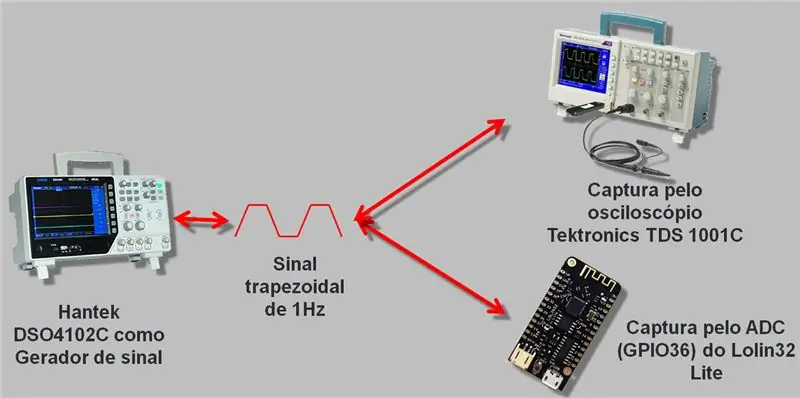
Koristio sam osciloskop s generatorom signala koji ide do 25 MHz, Hantek DSO4102C. Generirali smo val koji su očitali ESP A / D i osciloskop. Prikupljeni podaci zabilježeni su u csv -u i u proračunskoj tablici koju ću ostaviti na kraju članka za preuzimanje.

Korak 5: Upotrijebite znak

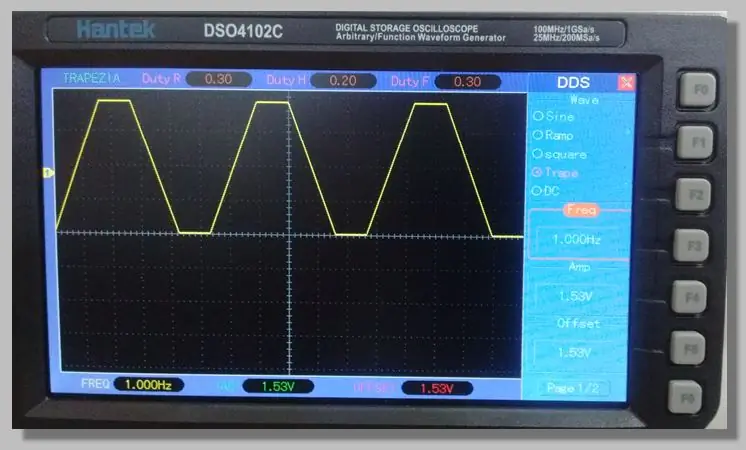
Odabrali smo niskofrekventni trapezni signal koji omogućuje pristup rampama koje prolaze kroz cijeli raspon pretvorbe. To omogućuje veliki broj uzoraka na ovim rampama.

Korak 6: Podaci dobiveni osciloskopom

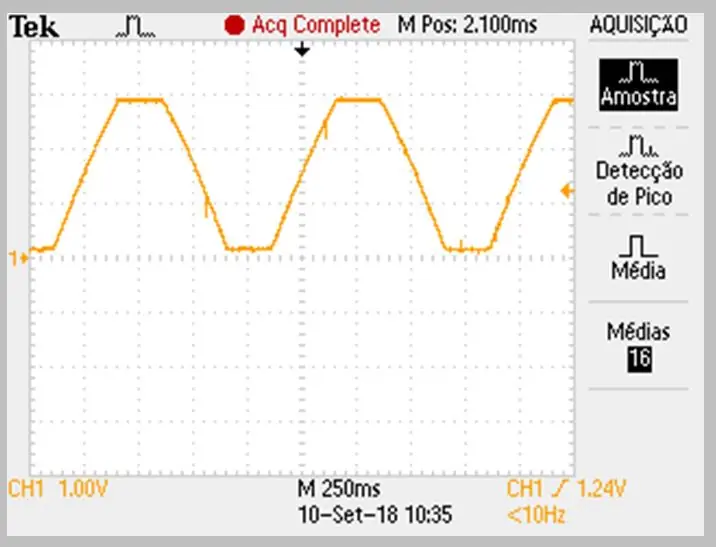
Slika snimanja izvedena je osciloskopom. Podaci su pohranjeni u csv datoteci. Obratite pozornost na blagu zakrivljenost na rastućim i padajućim rampama signala.

Korak 7: Podaci dobiveni osciloskopom (csv datoteka u Excelu)

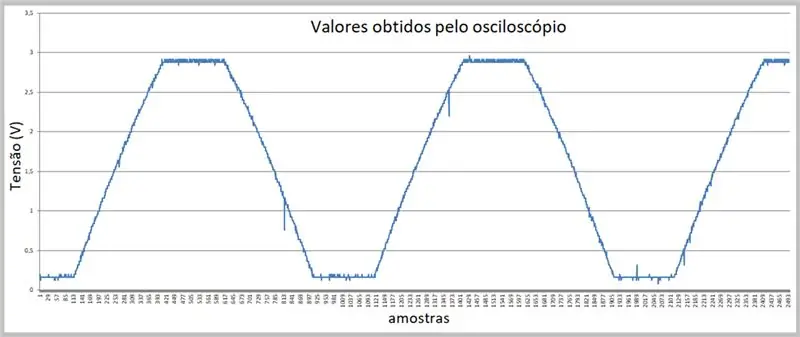
Ovdje imamo uzorke.

Korak 8: Podaci dobiveni od ADC -a

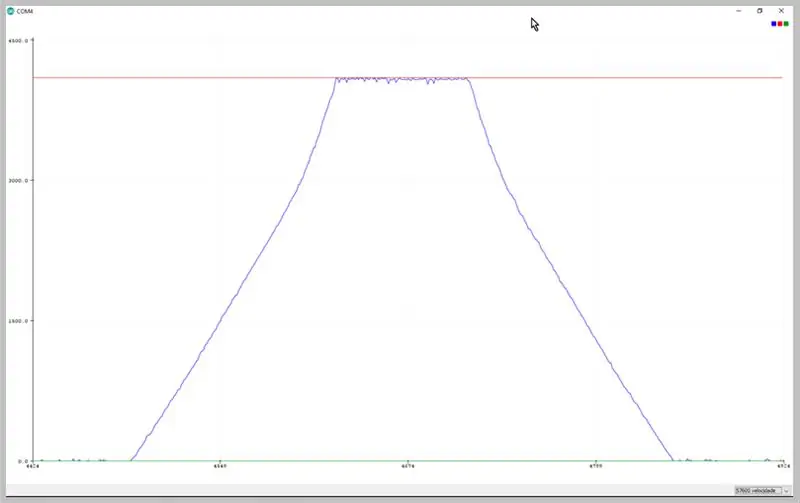
Promjenom brzine prijenosa serijskog zapisa možemo vidjeti podatke koje je zabilježio ADC. Promatrajte deformaciju trapeznog signala.

Podaci uočeni na Arduino IDE serijskom ploteru

Korak 9: Podaci dobiveni od ADC - Excel

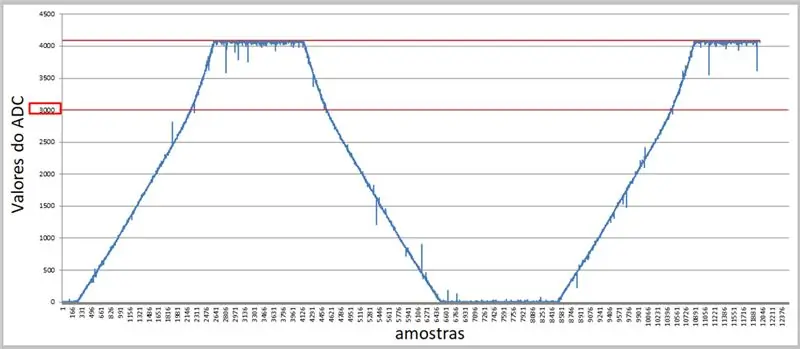
Koristeći veću stopu i serijski terminal, možemo zabilježiti vrijednosti i primijeniti ih u Excelu za naše usporedbe.

Korak 10: Usporedba rampi za uspon

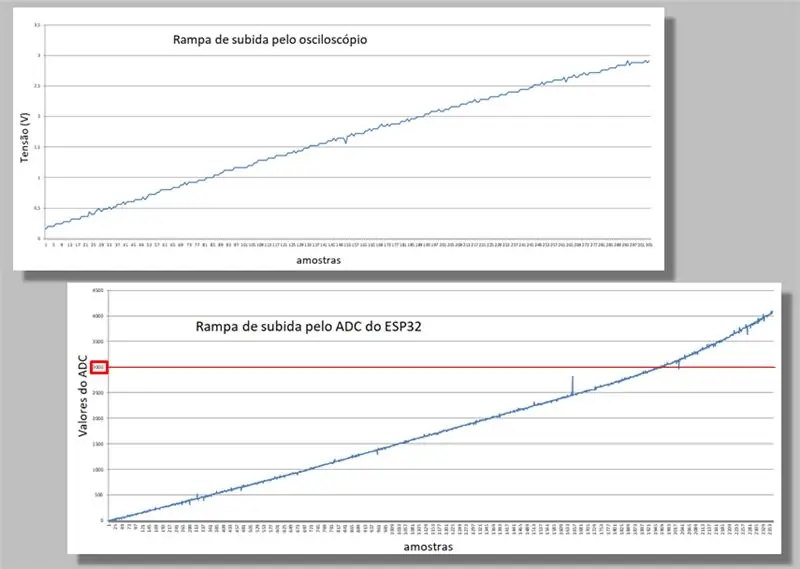
Uspoređujemo dvije penjalice za dva hvata.

Obratite pozornost na zakrivljenost koja se javlja na obje rampe.

Također imajte na umu da za istu rampu imamo mnogo više uzoraka ESP32 nego s osciloskopa.

Korak 11: Izjednačavanje broja uzoraka

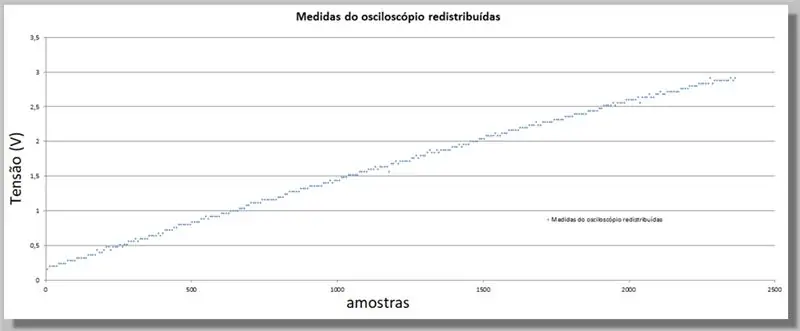
Budući da je ESP32 dao veći broj uzoraka od osciloskopa, moramo izjednačiti te vrijednosti jer će one poslužiti kao indeks za usporedbu dviju krivulja.

Za to ćemo napraviti izravnu usporedbu.

Imamo 305 uzoraka za osciloskopsku rampu i 2365 uzoraka za ADC rampu.

Budući da su rampe istog raspona, možemo reći da imamo približno 7,75 uzoraka ADC -a za svaki osciloskop.

Množenje indeksa svakog uzorka osciloskopa ima istu krivulju, ali s indeksima ekvivalentnim ADC -u i preraspodijeljenim podacima.

Kako bismo popunili podatke koji nedostaju za nove pozicije, primijenit ćemo krivulju koja statistički odgovara poznatim podacima.

Korak 12: Popunjavanje praznina - linija trenda

Odabirom poznatih podataka (plave točkice) klikom i desnim gumbom miša odabiremo: "Dodaj liniju trenda …"

U prozoru koji se pojavi odabiremo polinomski tip (redoslijed 2 bit će dovoljan).

Također smo provjerili opcije "Prikaži jednadžbu u grafikonu" i "Prikaži vrijednost R-kvadrata u grafikonu".

Kliknemo "Zatvori".

Korak 13: Popunjavanje praznina - polinomska krivulja 2. stupnja

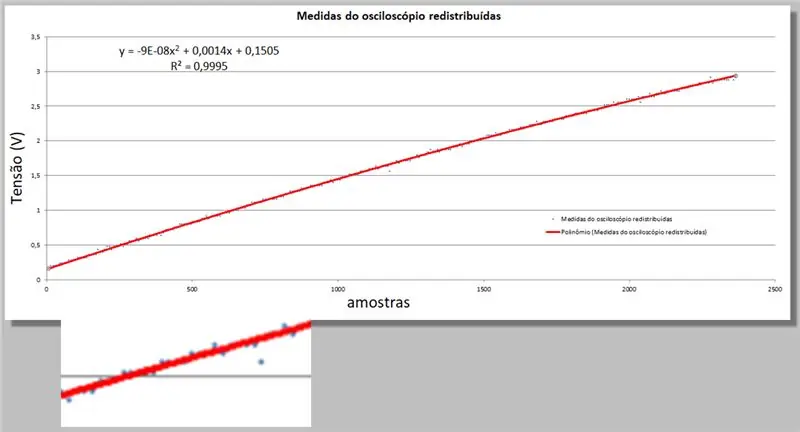
Excel nam daje dvije nove informacije; jednadžba drugog reda koja najbolje odgovara podacima i jednadžba na R-kvadratu koja kvantificira tu adekvatnost.

Samo zapamtite da što je bliže 1, jednadžba je prikladnija.

Nemojmo se upuštati u matematiku koja je u pitanju, samo je upotrijebimo kao alat.

Korak 14: Popunjavanje praznina - Procjena funkcije

Popunimo praznine u uzorkovanju podacima generiranim jednadžbom. Zatim ih usporedite točku po točku.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Napon osciloskopa = -9E -08 * indeks2 + 0, 0014 * indeks + 0, 1505

Korak 15: Pretvaranje napona osciloskopa u ekvivalentnu vrijednost za usporedbu s ADC -om

Iskoristimo to za transformaciju vrijednosti napona osciloskopa u ekvivalentnu vrijednost ADC -a.

Kako je najveća vrijednost dobivena u ADP -u ESP32 bila 4095, što je ekvivalent očitavanju od 2,958 V za isti indeks, možemo reći da:

Svaki volt u mjerenjima osciloskopa jednak je približno 1384,4 jedinica AD. Stoga možemo pomnožiti sva mjerenja osciloskopa s ovom vrijednošću.

Korak 16: Usporedba dvije dobivene rampe

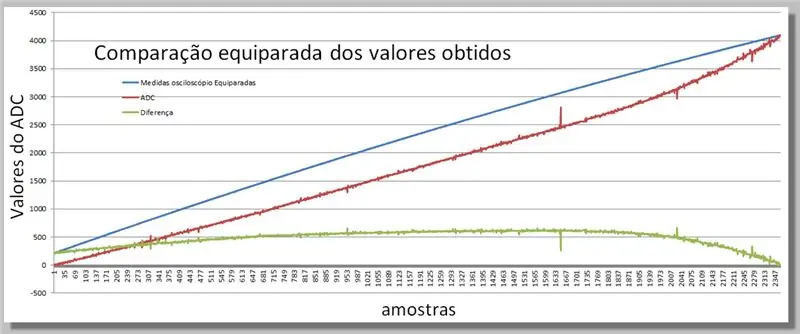
Vizualizacija razlika dobivenih u dva čitanja.

Korak 17: Ponašanje razlike čitanja ADC -a (POGREŠKA)

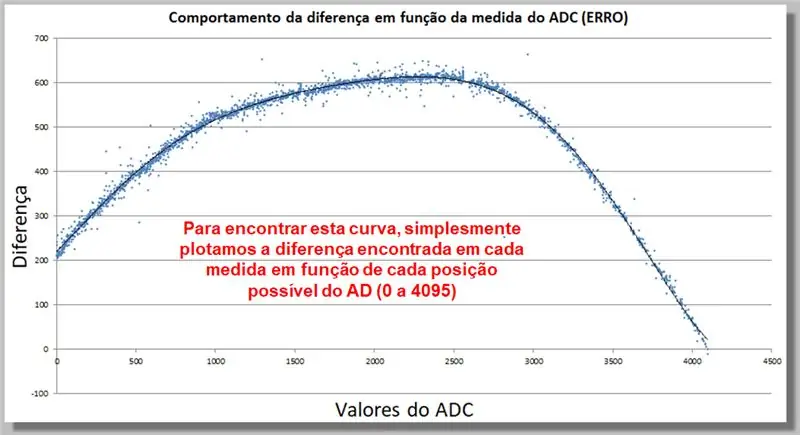
Donja krivulja prikazuje kako se razlika u očitanju ADC -a ponaša kao funkcija mjerenja. Ova zbirka podataka omogućit će nam da pronađemo funkciju korekcije.

Da bismo pronašli ovu krivulju, jednostavno iscrtamo razliku koja se nalazi u svakoj mjeri kao funkciju svakog mogućeg položaja AD (0 do 4095).

Korak 18: Različito ponašanje čitanja ADC -a - pronalaženje korekcijske funkcije

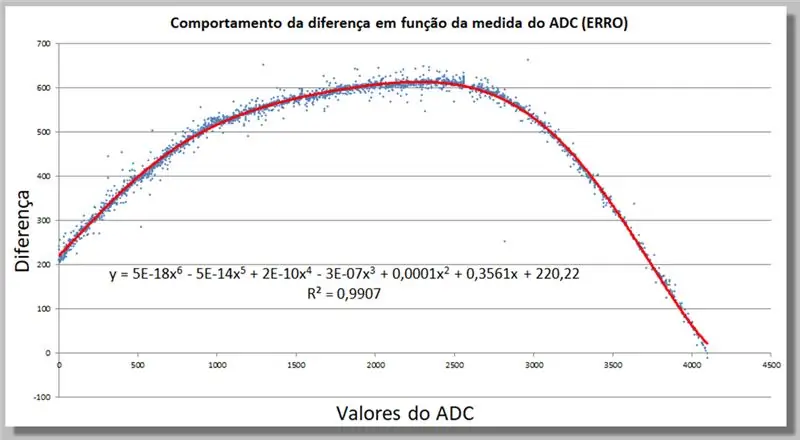
U Excelu možemo odrediti korekcijsku funkciju dodavanjem linije trenda, sada višeg stupnja, sve dok se dovoljno ne uklapa u naše podatke.

Korak 19: Korištenje drugog softvera

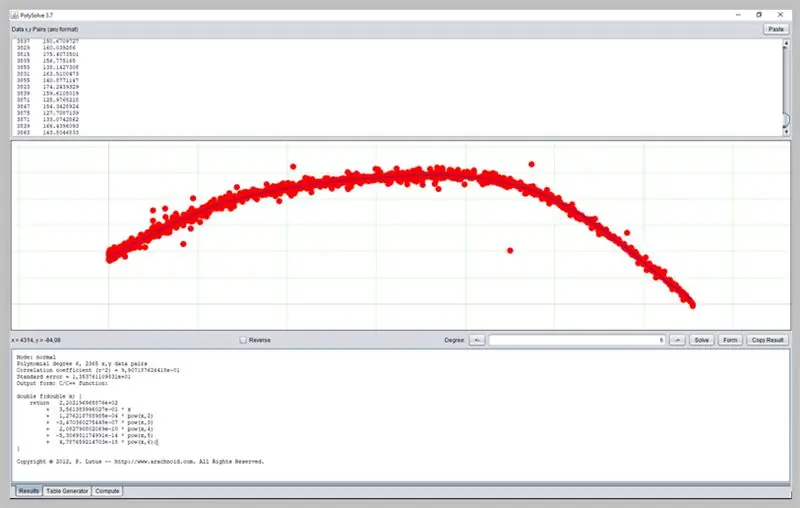
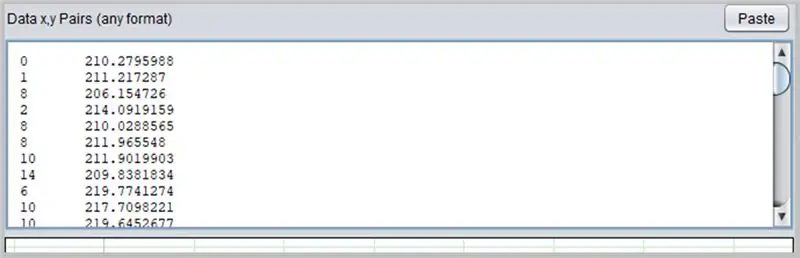
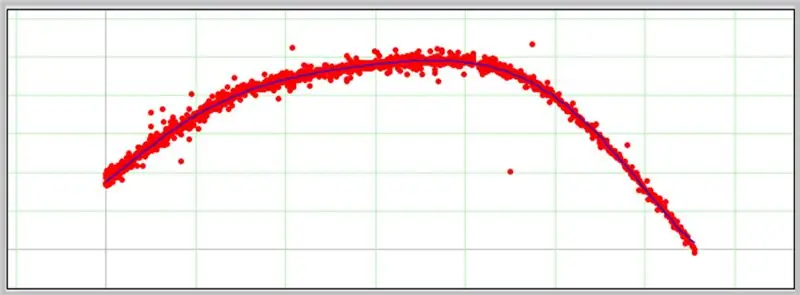
Drugi zanimljiv softver za određivanje krivulja je PolySolve, koji se može koristiti izravno na poveznici: https://arachnoid.com/polysolve/ ili preuzeti kao Java aplikaciju.

Omogućuje primjenu polinomskih regresija višeg stupnja i isporuku formatirane funkcije, kao i drugih funkcionalnosti.

Da biste ga koristili, jednostavno unesite podatke u prvo tekstualno polje. Podaci moraju slijediti redoslijed X, Y odvojen zarezom ili tabulatorom. Budite oprezni pri ispravnoj uporabi točke kao decimalne točke.

Tablica će se pojaviti u sljedećem okviru ako su uneseni podaci ispravno formatirani.

Evo kako je prošla naša krivulja pogreške ADC -a.

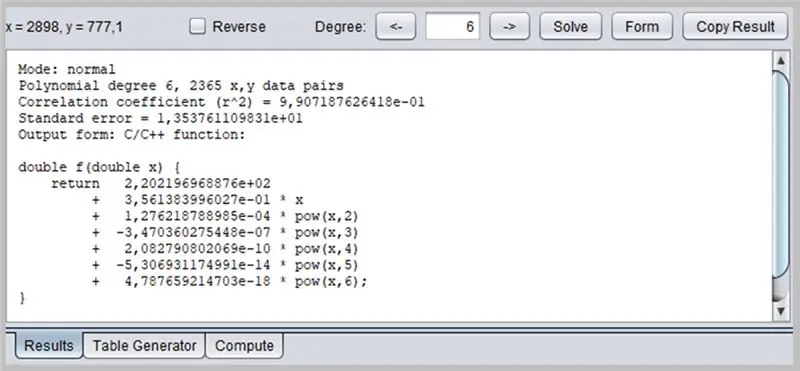
Ovaj će prozor prikazati rezultat regresije, uključujući podatke o prikladnosti funkcije, koji pak mogu imati formatirane svoje izlaze na nekoliko načina: kao C / C ++ funkciju, popis koeficijenata, funkciju napisanu na Javi itd.

Napomena: Obratite pažnju na decimalne separatore

Korak 20: Konstante i postavljanje ()

Ovdje ističem GPIO koji se koristi za analogno snimanje. Pokrećem serijski port, kao i pin određen za analogno snimanje.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Pokretanje serijskog portala za debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Korak 21: Petlja () i funkcija korekcije

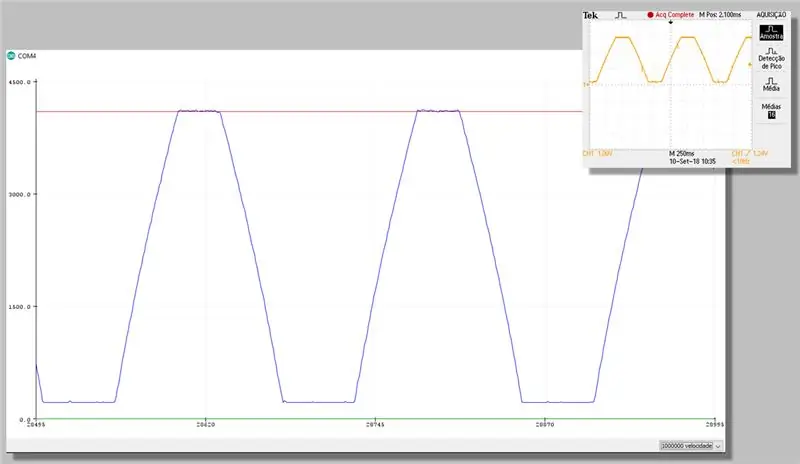
Snimamo podešeni napon i ispisujemo vrijednosti sa ili bez ispravnih ispravki.

void loop () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Uočite u retku 12 da imamo mogućnost ispisa podataka uz dodatak funkcije razlike f (analogna_vrijednost).

Korak 22: Korištenje funkcije PolySolve Correction

Ovdje koristimo funkciju PolySolve unutar Arduino IDE -a.

/* Način rada: normalni Polinomski stupanj 6, 2365 x, y parovi podataka Koeficijent korelacije (r^2) = 9, 907187626418e-01 Standardna pogreška = 1, 353761109831e+01 Izlazni oblik: C/C ++ funkcija: Copyright © 2012, str. Lutus - https://www.arachnoid.com. Sva prava pridržana. */ double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Obratite pažnju na promjenu zareza po točka kao decimalnog razdjelnika.

Korak 23: Snimanje uz ispravak - Serijski ploter

Korak 24: Računski troškovi

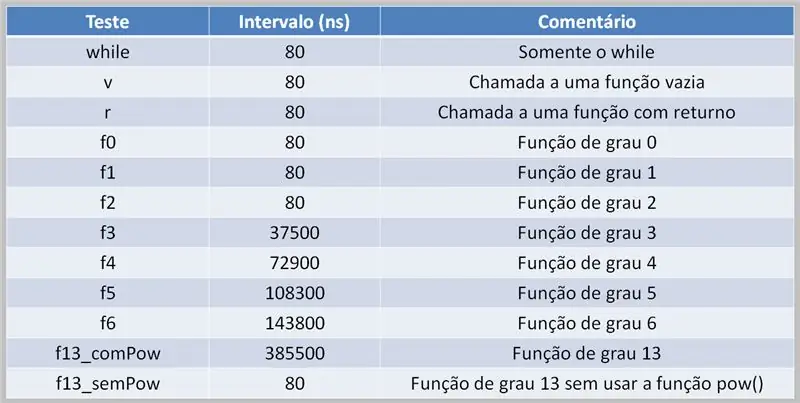
Za izvođenje polinomskih izračuna potrebno je da procesor obavi ovaj zadatak. To može dovesti do kašnjenja u izvođenju, ovisno o izvornom kodu i raspoloživoj računalnoj snazi.

Ovdje vidimo tablicu rezultata testa korištenjem višestepenih polinoma. Uočite razliku između vremena kada je funkcija pow () korištena i kada nije.

Korak 25: Testni kod - Postavljanje () i Pokretanje petlje ()

Ovdje imamo kôd korišten u našem testu.

void setup () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0.0; // contador de chamadas

Korak 26: Testni kod - Petlja () i obrada

Koristio sam funkciju micros () da dobijem vrijednost u mikrosekundama.

// ============= inicia o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / kvantidada; // determina o intervalo que se passou para cada iteração // ============= finaliza o processo

Korak 27: Testni kod - Petlja () - Rezultati

Tiskamo vrijednost vraćenu iz funkcije ocjene 13 sa i bez POW -a radi usporedbe, kao i interval obrade.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM i funkcijski POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (agora, 6); }

Korak 28: Testni kôd - korištene funkcije

Prazne funkcije (samo s povratkom) stupnjeva 0 i 1.

// FUNÇÃO VAZIAdvostruki v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 double f1 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Funkcije 2., 3. i 4. stupnja.

// FUNÇÃO DE GRAU 2dvostruki f2 (dvostruki x) {povratak 2,202196968876e + 02 + 3,561383996027e-01 * x + 1,267218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * pow (x, 4); }

Funkcije razreda 5 i 6.

// FUNÇÃO DE GRAU 5dvostruki f5 (dvostruki x) {povratak 2,202196968876e + 02 + 3,561383996027e-01 * x + 1,267218788985e-04 * pow (x, 2) + -3,470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * pow (x, 4) + -5,306931174991e-14 * pow (x, 5) + 4,787659214703e-18 * pow (x, 6); }

Funkcija stupnja 13 pomoću POW -a.

// FUNÇÃO DE GRAU 13 USANDO O POWdvostruki f13_comPow (dvostruki x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Funkcija stupnja 13 bez upotrebe POW -a.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Korak 29: Datoteke

Preuzmite datoteke:

PDF

INO

Proračunska tablica