Sadržaj:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 09:33.
- Zadnja promjena 2025-06-01 06:09.
Este programa es una tarea que me dejaron en mi clase final de Tecnología, en el grado 11. El propósito era lograr crear, por medio del uso de Python y sus librerías, un programa que me permitiera traficar un trapecio a partir de una función y unos puntos de la misma, que serán todos dados por el usuario. Para esto, se usó Python 2.7.11. Nastavak se eksplicira paso a paso el proceso que se siguió, ali konačno dando el producto final (el código) con el propósito que se entienda lo hecho.
Korak 1: Comprensión Y Planteamientos
Bueno, lo primero que se hizo fue comprender qué era lo que se quería hacer, y el procedimiento que se tenía que seguir para lograrlo. Pues bien, para comenzar, hay que aclarar el objetivo que se propuso. En palabras simples, la meta era, como ya se ha dicho, crear un programa que, a partir de una función dada por el usuario y unos puntos de esta misma, se lograra graficar un trapecio, dar su área, y mostrar la misma función. Para esto, se comenzará priznaiendo conocimientos previos- lugar en el cual se organizarán los pasos a seguir-, y luego se creará el programa.
Korak 2: Conocimientos Previos
En este punto, se quiere obtener todo lo que se necesitará para ejecutar el programa, con el propósito de que, más adelante, solo se acople todo con facilidad.
1. Librerías y programas necesarias
- Claramente, se debe tener Python (za preuzimanje kliknite ovdje)
- Luego de haber descargado Python, se deben tener las bibliotecas necesarias para usar el programa. Estas serán numpy y mathplotlib. La forma de descargar estos dos puede ser vista, respectivamente, dando click aquí o aquí.
** SAVJET: Si necesitan cualquier asesoría, buscar en google en youtube, ahí hay muchas opciones e instrucciones. Sin embargo, siempre recuerden descargar de fuentes oficiales, para evitar algún virus. **
2. Organizacija: ¿Qué datos y comandos necesito?
- PRESENTACIÓN. Antes que nada, hay que lograr que el usuario comprenda la utilidad del programa, y hay que presentárselo. Para esto se necesita un comando básico que muestre mensajes a la pantalla, llamado print.
-
RECOLECCIÓN DE DATOS. Para cumplir el propósito planteado, el usuario me tiene que dar una funkción y también dos datos x para ubicar dos vértices del trapecio dentro de la función. Los otros dos serían simplemente las bases, que estarán ubicadas en y = 0.
Para lograr esto, necesito sabre cómo hacer que el usuario ingrese datos, cómo evaluar una función, y cómo crear ubicaciones dentro de un plano cartesiano
- PODRUČJE DEL TRAPECIO. Además, ya teniendo lo básico claro, hay que sabre cómo encontrar el área del trapecio. Para esto, se debe conocer la fórmula para encontrar dicha área, y se debe poder usar un comando para mostrársela al usuario.
-
GRAFICACIÓN
- GRAFICACIÓN DEL TRAPECIO. Acá se debe encontrar cómo puedo traficar una figura usando las librerías que tengo y la información dada.
- GRAFICACIÓN DE LA FUNCIÓN. Konačno, se debe comprender cómo se logra mostrar toda la función dentro de la gráfica del trapecio.
Ya teniendo esto claro, se sigue a la ejecución de estos datos y la creación del código.
Korak 3: Predstavljanje Del programa Al Usuario Y Datos Básicos

Como ya se dijo, este paso es muy simple, ya que consiste en básicamente presentar el programa al usuario. Griješni embargo, aunque sea simple, es muy relevante. El objetivo de estos programas es que sean útiles para alguien, y gracias a esto, lo son. Por esta razón, en mi caso, con el uso de print, yo simplemente uvodite la utilidad del programa. No hay que ser especialmente queridos ni nada, lo más relevante es que el usuario entienda de qué le servirá el programa. También, antes que nada, hay que Introducir las librerías como se muestra en la imagen.
SAVJET: Se recomienda usar comentarios (con numerales ##) para organizar el programa y entender cada paso.
NO SE DEBEN USAR TILDES, YA QUE SI SE HACE SE CERRARÁ PYTHON
Korak 4: Recolección De Datos
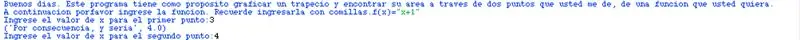
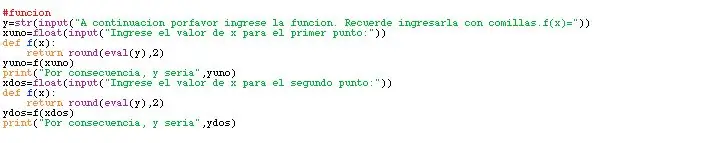
Ahora, ya habiendo presentado el program, es hora de construir los datos principales. Los datosi su van a almacenar en cajas o en varijable. Sin embargo, como estos dependen del usuario, hay que preguntarlos y, luego de preguntarlos, se pueden conseguir otros. En la imagen se puede ver el procedimiento que se hizo para conseguir los datos, con el código, y el resultado que debería salir en la pantalla por el momento.
Korak 5: Área Del Trapecio
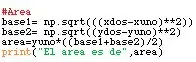

Este paso es, realmente, uno de los más jednostavnosti. Con la fórmula de área para un trapecio, se ingresan las varijable necesarias, se calcula, y se presenta al usuario con print. Como se puede ver, fue necesario encontrar las bases, para lo cual se usó la fórmula de distancia entre dos puntos. En las imágenes se puede ver el código y el resultado.
Korak 6: Graficación Trapecio
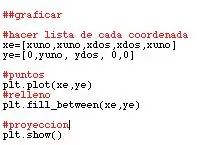
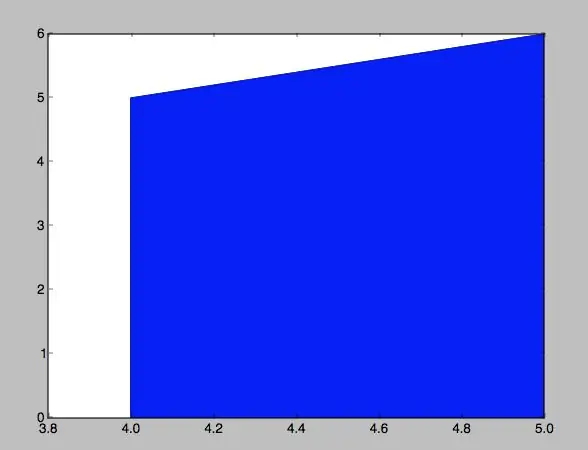
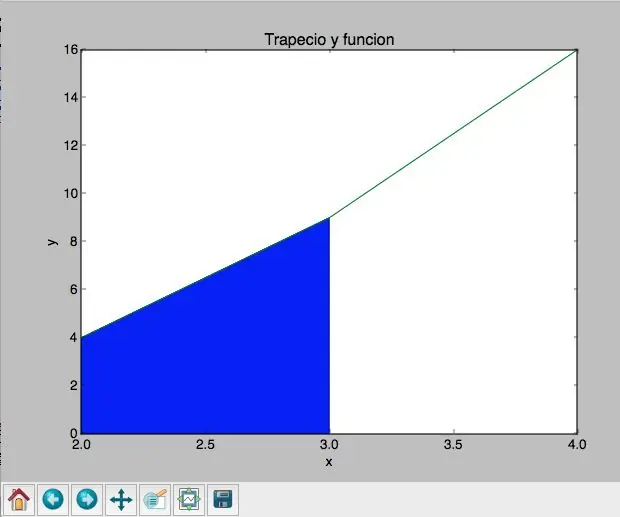
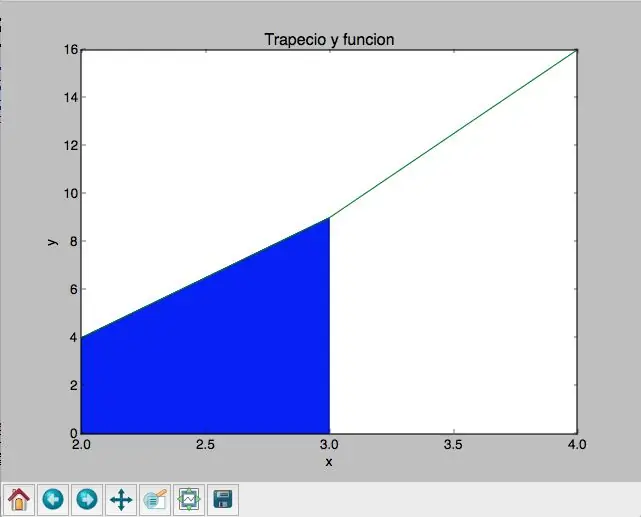
Ya teniendo todos los datos, lo único que falta es graficar tanto el trapecio como la función. En mi opinión, graficar el trapecio fue mucho más más simple, razón por la cual lo explicaré primero.
Como se sabe, con los datos priznaje ya tengo los cuatro puntos del trapecio. Ahora, me toca encontrar una forma de crear una figura y llenarla. Para esto, se crearon listes con los datos respectivos de x y y- llamadas xe y ye- con el propósito de generar los puntos. Luego, se puso plt.plot (xe, ye), lo cual me da los puntos pedidos. Konačno, se pidió que se llenara el espacio dentro de estos puntos, como se puede ver en las fotos. En las imágenes, de hecho, se mostrará tanto el código como el resultado final.
Korak 7: Grafica Función
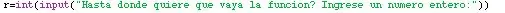

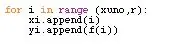
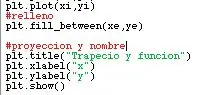
Ahora, sigue la parte que, a mi, más se me dificulto: graficar la función. Para esto, usé el comando for i in range, y por ende tuve que delimitar el dominio de la función. Decidí que el dominio la función va a empezar en el menor punto del trapecio, y que el usuario tendrá la libertad de determinar dónde terminina la función. para esto, me tocó hacer algunos cambios en la recolección de datos con el usuario, los cuales se pueden ver en las imágenes. Luego, ya teniendo esto, se crearon las listas xi y yi (previas a la función for, porque o sino no sirve) para que acá se añadan elementos a la lista. Konačno, se usó za, y se usó dodati para agregar tanto los datos de i (que son los datos de xi) como los datos de f (x) (que son los de y). Luego, se puso un título a la gráfica, se nombraron los ejes y se usó plt.plot para traficar todo. En las fotos are mostrarán algunos cambios, el código final y el resultado.
Korak 8: Codigo Finale
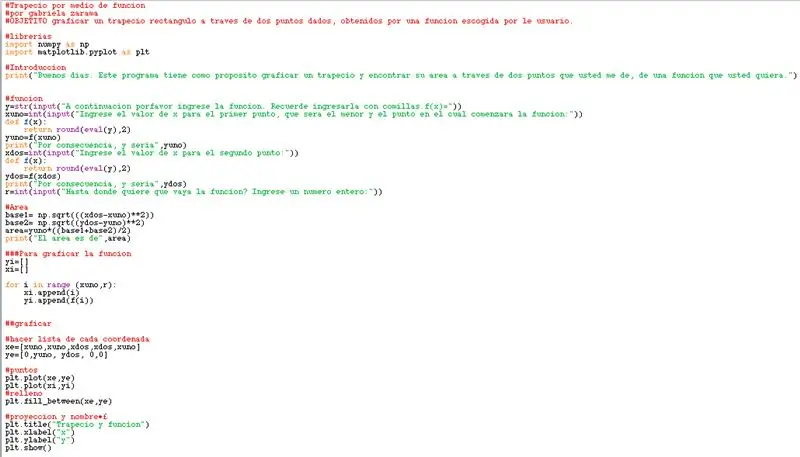
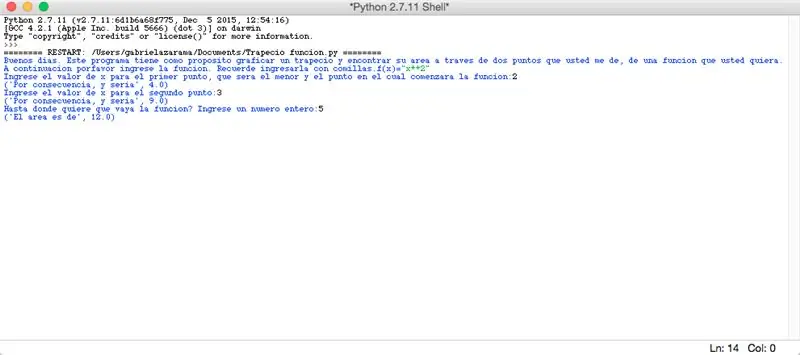
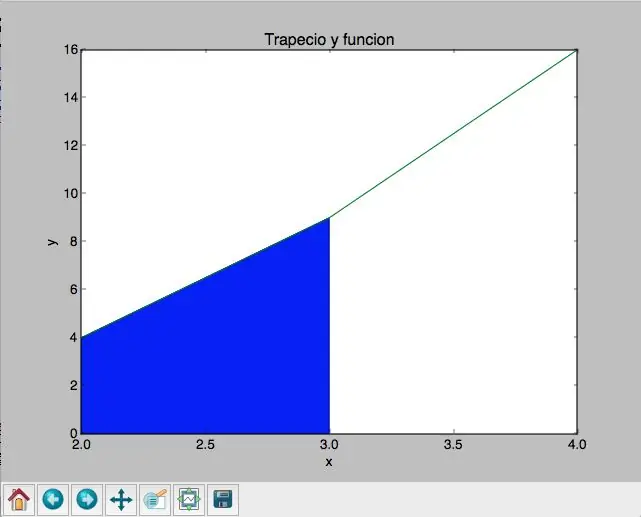
Konačno, el program quedó de la siguiente forma:
#Trapecio por medio de funcion#por gabriela zarama
#OBJETIVO graficar un trapecio rectangulo a traves de dos puntos dados, obtenidos por una funcion escogida por le usuario
#librerije
uvoz numpy kao np uvoz matplotlib.pyplot kao plt
#Uvod
print ("Buenos dias. Este programa tiene como prijedito graficar un trapecio y encontrar su area a traves de dos puntos que usted me de, de una funcion que usted quiera.")
#funkcija
y = str (input ("A continuacion porfavor ingrese la funcion. Recuerde ingresarla con comillas.f (x) =")) xuno = int (input ("Ingrese el valor de x para el primer punto, que sera el menor y el punto en el cual comenzara la funcion: "))
def f (x):
povratna runda (eval (y), 2)
yuno = f (xuno)
print ("Por consecuencia, y seria", yuno)
xdos = int (input ("Ingrese el valor de x para el segundo punto:"))
def f (x):
povratna runda (eval (y), 2)
ydos = f (xdos)
print ("Por consecuencia, y seria", ydos)
r = int (input ("Hasta donde quiere que vaya la funcion? Ingrese un numero entero:"))
#Područje
base1 = np.sqrt (((xdos-xuno) ** 2)) base2 = np.sqrt ((ydos-yuno) ** 2) area = yuno*((base1+base2)/2) print ("El area es de ", područje)
### Para graficar la funcion
yi = xi =
za i u rasponu (xuno, r):
xi.append (i)
yi.append (f (i))
## graficar
#hacer lista de cada coordenada
xe = [xuno, xuno, xdos, xdos, xuno]
ye = [0, yuno, ydos, 0, 0]
#puntos plt.plot (xe, da)
plt.plot (xi, yi)
#relleno
plt.fill_between (xe, ye)
#proyeccion y nombre
plt.title ("Trapecio y funcion")
plt.xlabel ("x")
plt.ylabel ("y")
plt.show ()
Preporučeni:
Como Crear Un Programa En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: 5 koraka
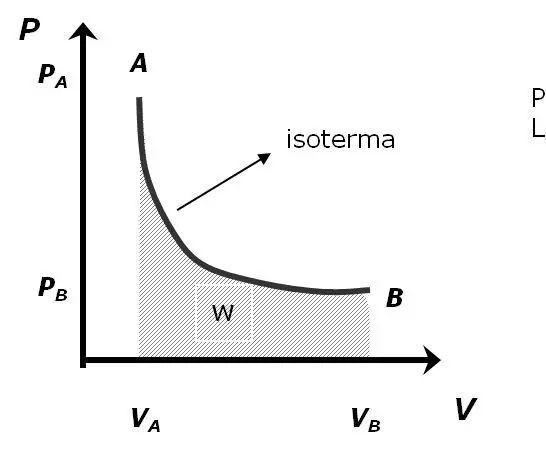
Como Crear Un Programa En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: En tutorial se enes ñ ara a calcular el area bajo una curva con datos importados desde un archivo. Para ello se calcula el area usando muchos trapecios sumados y se colorear á el područje bajo esta
Área De Un Trapecio: 6 koraka
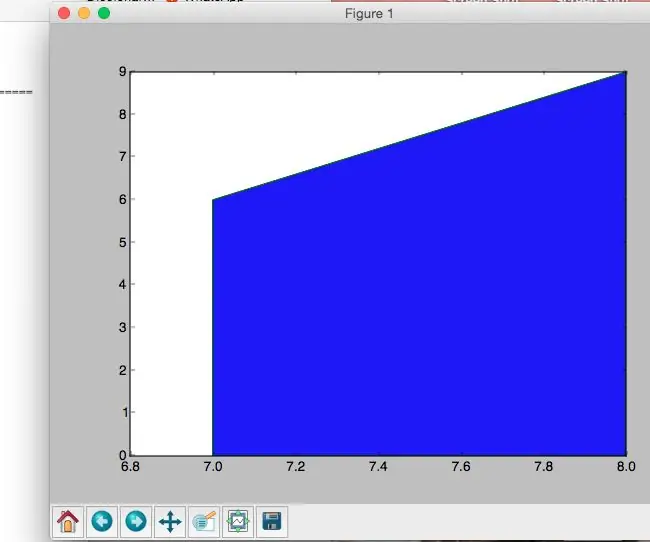
Área De Un Trapecio: Se create un script que permite calcular el á rea de un trapecio rect á ngulo. Partr de dos puntos (x1, y1) (x2, y2), formira se kao trapecio con las parejas ordenadas (x1,0) y (x2,0). El trapecio queda dibujado y sombreado
Cálculo Del Área Bajo La Curva De Una Función Con Python: 8 koraka
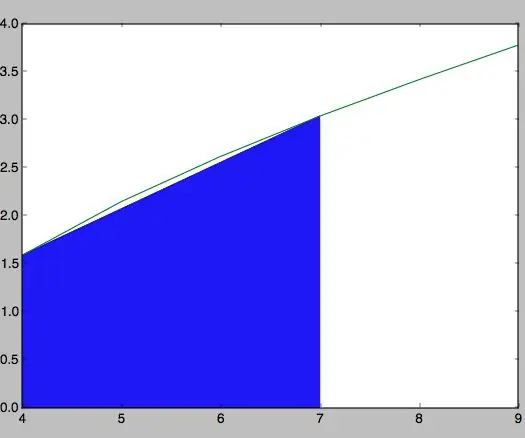
Cálculo Del Área Bajo La Curva De Una Función Con Python: Antes que nada, para desarrollar este programa debes instalar la plataforma Python desde su p á gina oficial :. Lo m á s preporučljivo es instalar la versi ó n 2.7.12 de 64 bita
Como Crear Un Programa De Python Que Grafique Cualquier Función Y Saque Un Área Especifica Debajo De Ella: 6 koraka

Como Crear Un Programa De Python Que Grafique Cualquier Función Y Saque Un Área Especifica Debajo De Ella: Este program permite al usuario Introducir cualquier funci ó n, graficarla y deterar un area especifica debajo de la misma
Dibujando Mí Entorno Con ADELE a Través Del Método Científico: 8 koraka

Dibujando Mí Entorno Con ADELE a Través Del Método Científico: Nuestro proyecto consiste en la enseñanza del método científico en enfocándonos en la asignatura de matemática, integrando la robótica como un material de apoyo (ADELE)
