Sadržaj:
- Pribor
- Korak 1: Postavite svoju glavnu metodu
- Korak 2: Izradite zaglavlje rekurzivne metode
- Korak 3: Izradite svoju početnu/osnovnu futrolu
- Korak 4: Rekurzivni korak
- Korak 5: Skratite problem
- Korak 6: Stvorite niz cijelih brojeva
- Korak 7: Nazovite metodu svojim nizovima
- Korak 8: Ispišite rezultate
- Korak 9: Čestitamo
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 09:33.
- Zadnja promjena 2025-01-23 14:47.
Rekurzija je vrlo koristan i vremenski učinkovit postupak koji može brzo riješiti problem s vrlo malo koda. Rekurzija uključuje metodu koju sami stvorite nazivajući skraćivanje izvornog problema.
Za ovaj primjer zbrajat ćemo niz od 10 cijelih brojeva, ali veličina može biti bilo koje duljine.
Pribor
Trebali biste znati osnovnu java sintaksu i imati IDE ili uređivač teksta koji će napisati vaš kôd za ovaj zadatak.
Korak 1: Postavite svoju glavnu metodu
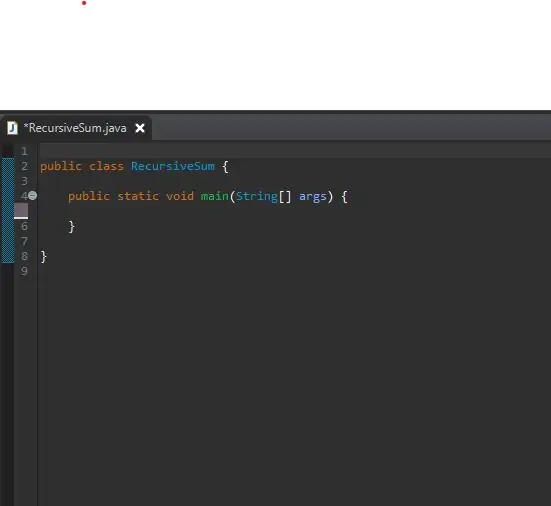
Za početak postavite svoju glavnu metodu u novostvorenu klasu. Svoj razred sam nazvao Rekurzivni zbroj. Ovdje ćete stvoriti niz cijelih brojeva i pozvati svoju rekurzivnu metodu.
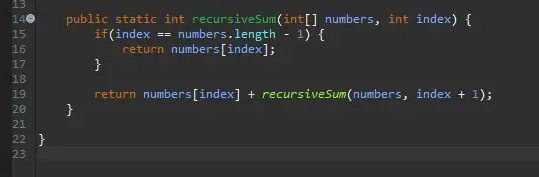
Korak 2: Izradite zaglavlje rekurzivne metode
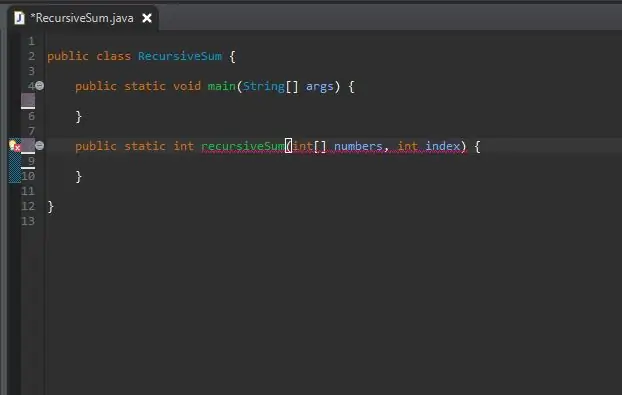
Izvan glavne metode stvorite zaglavlje metode za svoju rekurzivnu metodu.
Metoda je statična jer neće zahtijevati objekt na kojem će je koristiti.
Vrsta povratka je int, jer će niz koji ćemo koristiti biti pun na cijele brojeve. Međutim, to se može promijeniti na bilo koju vrstu broja koju polje sadrži.
Svoju metodu nazvao sam recursiveSum koja će uzeti dva parametra; niz cijelih brojeva i indeks koji ćemo zbroju dodati. Nazvao sam te parametre brojevima i indeksom.
Odmah ćete vidjeti pogreške i to je u redu. Oni će kasnije biti popravljeni.
Korak 3: Izradite svoju početnu/osnovnu futrolu
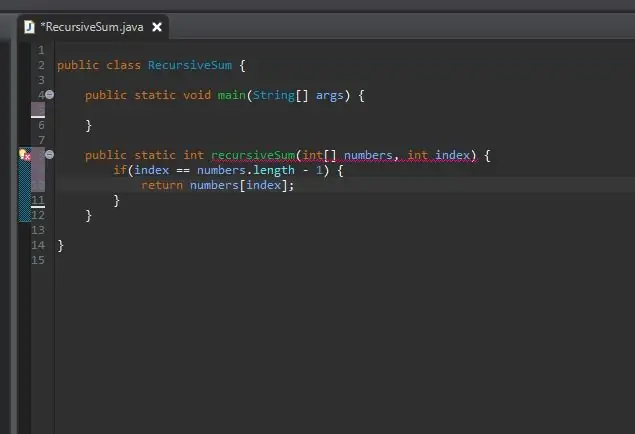
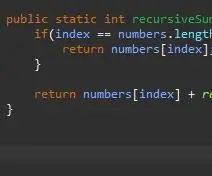
Rekurzivna metoda treba početni slučaj/osnovni slučaj. To je uvjet koji će spriječiti da se vaša metoda beskonačno poziva. Ovaj osnovni slučaj može se smatrati najjednostavnijim slučajem s kojim ćemo se susresti. U ovom slučaju, osnovni slučaj bit će kada smo na kraju našeg niza. Ako je trenutni indeks jednak duljini niza (minus 1 jer nizovi počinju brojati od 0, a ne 1), mi smo na kraju i jednostavno vraćamo taj element po tom indeksu.
Korak 4: Rekurzivni korak
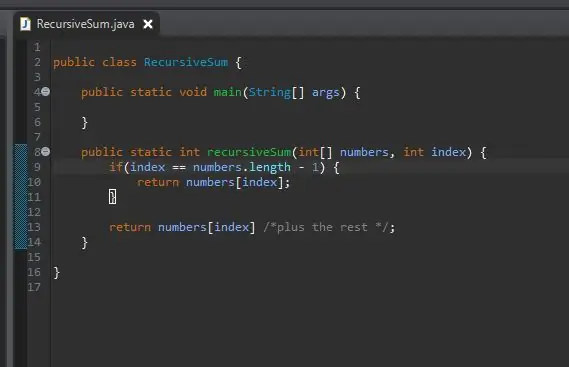
Kad dobijemo osnovni slučaj, sljedeći korak je naš rekurzivni korak. Tu se događa čarolija. Riješili smo slučaj kada je naš indeks jednak zadnjem elementu u našem nizu. Što ako nismo zadnji element u našem nizu? Što ako bismo mu jednostavno mogli reći da doda naš trenutni element plus sljedeći? Na kraju ćemo pogoditi kraj našeg niza i naš osnovni slučaj će stupiti na snagu.
Da bismo to postigli, jednostavno vraćamo naš trenutni indeks i "dodajemo ostatak" niza.
Korak 5: Skratite problem
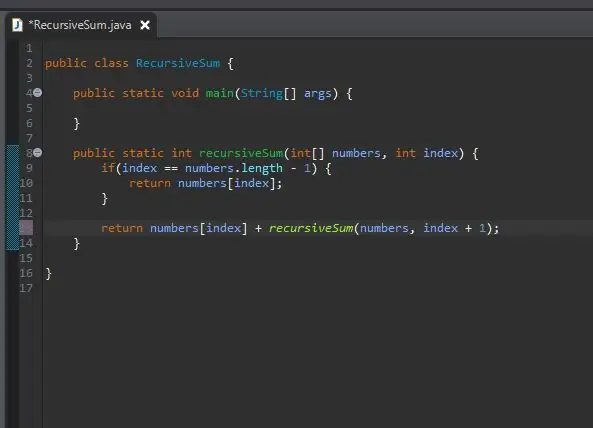
Kako jednostavno "dodamo ostalo"? Već imamo metodu koja će dodati određeni element; naša rekurzivnaSum () metoda! Možemo ga ponovno nazvati, ali promijenimo indeks koji zbrajamo.
Prolazimo u isti niz koji obrađujemo, ali prosljeđujemo sljedeći indeks iz našeg trenutnog indeksa. To činimo jednostavnim dodavanjem jednog u naš trenutni indeks, kao što je prikazano.
Korak 6: Stvorite niz cijelih brojeva
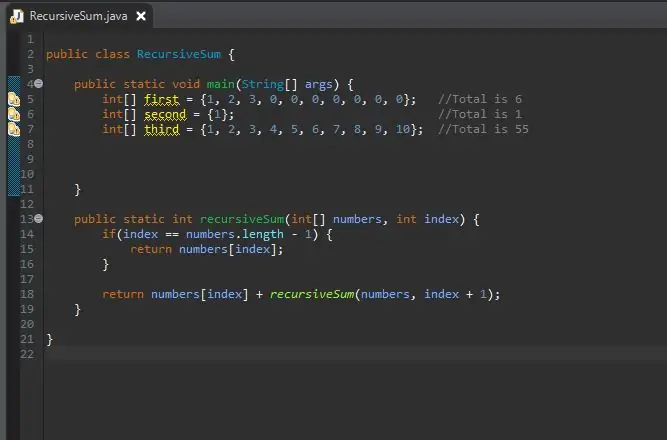
Sada kada je naša rekurzivna metoda zbrajanja dovršena, možemo stvoriti naš niz koji ćemo obraditi. Ovaj niz će biti u našem glavnom bloku metoda.
Veličinu polja možete odrediti koliko god želite. Napravio sam nekoliko različitih nizova različitih veličina i vrijednosti kako bih pokazao da radi ne samo na jednoj veličini.
Korak 7: Nazovite metodu svojim nizovima
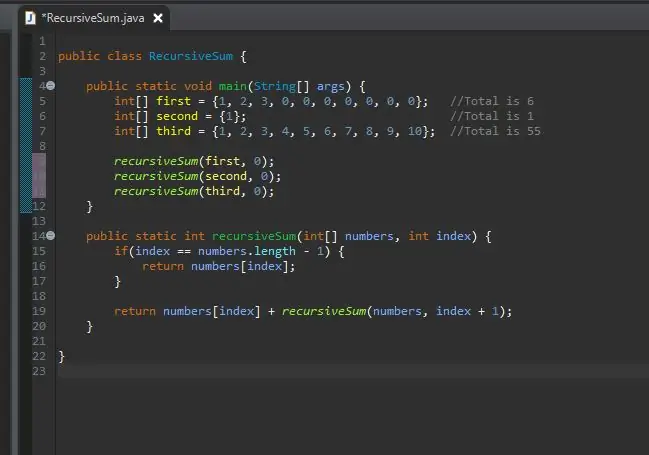
Sada možete pozvati svoju rekurzivnu metodu i proslijediti joj ove nizove. Sada možete pokrenuti svoj program.
Korak 8: Ispišite rezultate
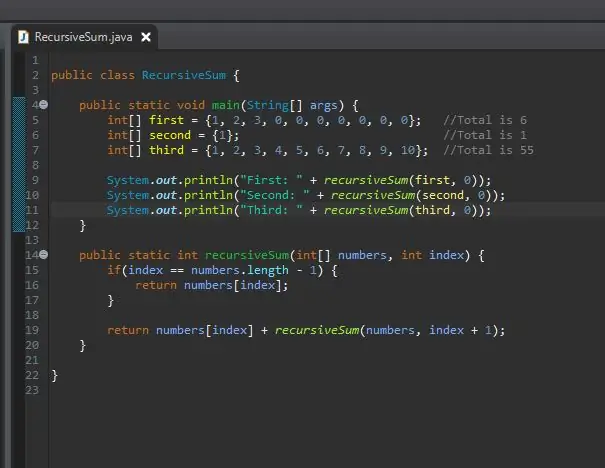
Ništa se nije dogodilo. Zašto? Rekurzivni zbroj vraća cijeli broj, ali ništa nismo učinili s tim cijelim brojem. Uradio je svoje, ali ne vidimo rezultat. Da bismo vidjeli rezultat, jednostavno ga isprintamo tako. Nakon pokretanja ovoga trebali biste vidjeti rezultate za svaki od vaših niza.
Korak 9: Čestitamo
Dovršili ste rekurzivnu funkciju. Slobodno promijenite veličinu svojih polja. Ako ga isprobate, primijetit ćete da se ruši kad imate prazan niz. Nismo to uzeli u obzir, ali to je sjajan način da poboljšate svoju rekurzivnu metodu.
Preporučeni:
Kako koristiti while petlju za ponavljanje niza u Javi: 9 koraka

Kako koristiti while petlju za ponavljanje niza u Javi: Danas ću vam pokazati kako koristiti Javu za stvaranje petlje While koja se može koristiti za ponavljanje kroz popis brojeva ili riječi. Ovaj koncept namijenjen je programerima početne razine i svima koji žele dobiti brzu nadogradnju na Java Loops i nizove
Korištenje RGB LED dioda za stvaranje niza boja: 12 koraka
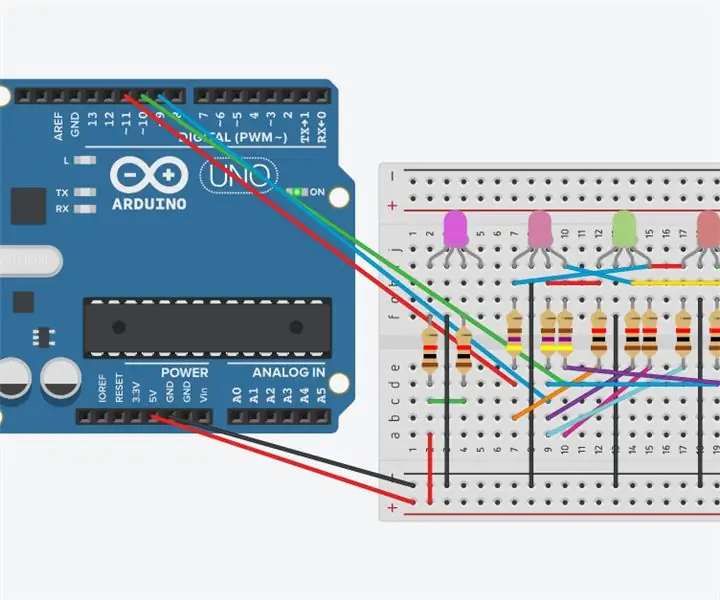
Korištenje RGB LED dioda za kreiranje nizova boja: Ove upute će vam pokazati kako koristiti RGB LED diode za stvaranje sekvenci boja pomoću Arduino Uno i koda. Tri RGB LED diode će tijekom vremena mijenjati boje, dok će ostale 2 RGB LED diode ostati iste boje
IR termalna kamera M5Stack koja koristi senzor za snimanje infracrvenog niza AMG8833: 3 koraka

IR termalna kamera M5Stack koja koristi senzor za snimanje infracrvenog niza AMG8833: Kao i mnogi, fascinirali su me termalni fotoaparati, ali oni su uvijek bili izvan mog cjenovnog raspona - do sada !! Dok sam pregledavao web stranicu Hackaday naišao sam na ovu kameru napravljenu pomoću M5Stack ESP32 modul i relativno jeftin
Napravite jednostavan EPUB od niza slika: 13 koraka

Napravite jednostavan EPUB od niza slika: Ovo nije tehnički projekt. Neću lutati o tome što EPUB jest, a što EPUB nije. Neću vam govoriti po čemu se razlikuje od drugih formata datoteka. EPUB je super cool format koji se može koristiti za mnogo, mnogo više od objavljivanja
Zatamnjivanje LED niza: 4 koraka
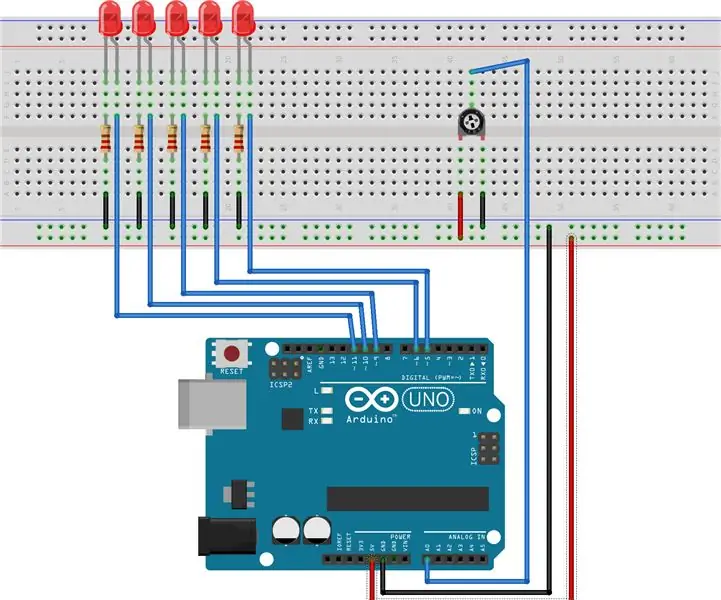
Svjetlosni niz s mogućnošću zatamnjivanja: Ovaj projekt postiže tri glavna cilja:- Očitavanje analogne vrijednosti s potenciometra- Zapisivanje analogne vrijednosti za svaki LED- Promjena svjetline svakog LED-a na temelju ulaza potenciometra Potrebni materijali:- 5 LED dioda- Potenciometar- (5) Otpor 220 ohma
