
Sadržaj:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 09:38.
- Zadnja promjena 2025-01-23 14:47.
Ovo uputstvo će obuhvatiti neke od najosnovnijih funkcija matlaba. Naučit ćete kako natjerati matlab da interno pokreće periodičnu funkciju i iscrtava te kako umjesto toga iz Excel datoteke izvući istu periodičku funkciju i iscrtati je. Ove su funkcije neke od najosnovnijih i široko korištene u matlabu. Ovo uputstvo je namijenjeno onima od vas koji nikada prije niste koristili matlab i samo trebate obaviti neke jednostavne zadatke s njim. Kôd istaknut na svakoj slici uključen je kao komentar tako da ga možete kopirati i zalijepiti. Slobodno uzmite ovaj kôd i izmijenite ga kako bi odgovarao vašoj prijavi.
Korak 1: Pokretanje Matlaba
Prvi korak je pokrenuti Matlab kako bismo mogli početi raditi s njim. Kada prvi put pokrenete matlab, to bi trebalo izgledati kao snimka zaslona u nastavku. Prvi korak je dodjeljivanje direktorija za rad Matlaba. Ovdje će program povući sve datoteke i tamo biste trebali spremiti sav svoj rad na matlabu. Preporučujem da napravite novu mapu negdje gdje ćete je zapamtiti i dati joj ime po nečemu što ćete prepoznati. Nakon što ste stvorili novu mapu, kliknite "…" koja se nalazi u gornjem desnom kutu zaslona kao što je istaknuto na drugoj slici. Ovo će otvoriti okvir za pregled kao što je prikazano na trećoj slici. Pronađite novu mapu koju ste stvorili na svom računalu i odaberite je. U ovom primjeru datoteka se naziva "370" i nalazi se na radnoj površini.
Korak 2: Stvaranje M-datoteke
Ono što moramo učiniti je stvoriti novu M datoteku. M datoteka funkcionira isto kao upisivanje koda izravno u matlab, ali možete spremiti i izmijeniti kôd te ga više puta pokretati. Prilikom unosa koda izravno u matlab upisujete svaki redak koda zasebno. U M datoteku napišete cijeli kôd, a zatim ga pokrenete odjednom. Za otvaranje nove M datoteke kliknite na datoteku. Postavite kursor na "Novo", a zatim kliknite na "Prazna M datoteka" kao što je prikazano na prvoj slici. Ono što se otvori trebalo bi izgledati kao druga slika. Budući da se ovaj kôd može izvoditi više puta, dobra je ideja zatvoriti sve i izbrisati sve varijable prije svakog pokretanja. To se postiže kroz dva retka koda: zatvori allclear all Kao što se vidi na trećoj slici, osigurava da je sve izbrisano i zatvoreno.
Korak 3: Stvaranje vremenskog vektora
Prvo što ćemo učiniti je stvoriti graf funkcije u matlabu. Prvi korak je stvaranje neovisne varijable. U ovom slučaju ćemo ga neko vrijeme zvati "t". Metoda koju ćemo koristiti za stvaranje ove varijable je izrada vektora. Vektor je u osnovi niz brojeva. Na primjer, 1, 2, 3, 4 bi bili kratki vektor. Kôd za stvaranje ovog vektora je: t = 0,1: 0,01: 10; Prvi broj, 0,1 odnosi se na početnu točku. Drugi broj, 0,01, odnosi se na veličinu koraka. Treći broj 10 odnosi se na krajnju točku. Dakle, ovaj vektor odgovara 0,1, 0,11, 0,12 … sve do 10. Da biste vidjeli je li stvaranje vektora uspjelo, kliknite zeleni gumb za pokretanje istaknut na drugoj slici. Ovo pokreće program. Da biste vidjeli naš vektor, idite na glavni prozor Matlaba. Pritisnite radnu površinu, a zatim mišem preko rasporeda radne površine, a zatim kliknite zadano kao što je prikazano na trećoj slici. Vaš bi zaslon trebao izgledati kao četvrta slika. Desno ćete vidjeti našu novostvorenu varijablu, t. Dvaput kliknite na nju i kao na petoj slici vidjet ćete niz stvorenih brojeva.
Korak 4: Pokretanje i iscrtavanje funkcije
Sada ćemo grafički prikazati funkciju stvorenu u matlabu. Prvi korak je stvaranje funkcije. Ovo je jednostavno kao ispisivanje željene matematičke funkcije. Primjer je prikazan na prvoj slici. Kôd koji se koristi za ovu funkciju je: y = sin (t)+4*cos (5.*t).^2; Razdoblje prije množenja u kosinusu i prije kvadrata kosinusa recite matlabu da izvrši te funkcije jednostavno na vrijednostima vremenskog vektora, a ne da vremenski vektor tretiramo kao matricu i pokušamo na njoj izvoditi matrične funkcije. Sljedeći korak je stvaranje same figure. To se postiže pomoću koda prikazanog na drugoj slici. Redoslijed varijabli u naredbi plot vrlo je važan pa svakako postavite svoj kôd kao što je dolje postavljen.figureh = axes ('fontsize', 14); plot (t, y, 'linewidth, 2) xlabel ('Time (s)') ylabel ('Y Value') Naslov ('Y Value vs Time') na mreži Konačno, samo ponovno kliknite zelenu strelicu za pokretanje i brojka bi se trebala pojaviti kao na trećoj slici.
Korak 5: Izvlačenje podataka iz programa Excel
Sada ćemo stvoriti isti grafikon kao i prije, ali uvozom podataka o funkciji iz Excel proračunske tablice. Prva slika je snimak zaslona Excel tablice koja će se koristiti. To su potpuno iste podatkovne točke stvorene u matlabu u prethodnim koracima, upravo napravljene u excelu. Za početak možemo izbrisati kôd koji stvara naš vremenski vektor i kôd za našu funkciju iz prethodnih koraka. Vaš kôd bi sada trebao izgledati kao druga slika. Umetnite kôd kao što je prikazano u gornjem crvenom okviru treće slike. Ovo je kod za čitanje excel datoteke. "A" se odnosi na matricu koja će uključivati sve brojeve u proračunskoj tablici, a "B" uključuje sav tekst iz proračunske tablice. Varijable t i y izvlače se iz prvog i drugog stupca kako je prikazano u kodu. [A, B] = xlsread ('excelexample.xlsx'); t = A (:, 1); y = A (:, 2 Kôd slike također se može izmijeniti kako je prikazano u donjem crvenom okviru na trećoj slici. Ovo će zapravo izvući naslov grafikona i oznake osi iz proračunske tablice i staviti ih na svoj grafikon. Xlabel (B (2)) ylabel (B (3)) Title (B (1)) Zadnja stvar koju trebate učiniti je pokrenuti program opet i vidjet ćete istu figuru kako se vidi na posljednjoj slici.
Korak 6: Izrada spektra
U ovom koraku ćemo koristiti matlab za stvaranje specgrama čitanjem wav zvučne datoteke. Spekgram se ponekad naziva "2.5D graf", jer koristi dvodimenzionalni graf, s dodatkom boje za prikaz amplitude. Boja pruža više detalja nego jednostavan 2D grafikon, ali ne i detalje 3D grafikona, otuda i izraz "2.5D." Funkcija specgrama matlaba uzima skup podatkovnih točaka iz wav datoteke i izvodi Fourierovu transformaciju na točke za određivanje frekvencija prisutnih u signalu. Za ovu instrukciju nije važno znati kako funkcionira Fourierova transformacija, samo znajte da će spektrogram prikazati koje su frekvencije prisutne i koliko su jake s obzirom na vrijeme. Funkcija prikazuje vrijeme na osi X i frekvenciju na osi Y. Jačina svake frekvencije prikazana je bojom. U ovom slučaju wav datoteka je zvučni zapis komada metala koji se udara, a zatim se vibracije metala bilježe kao zvuk. Pomoću specgrama lako možemo odrediti rezonantnu frekvenciju komada metala, jer će to biti frekvencija koja s vremenom traje najduže. Da biste izvršili ovaj zadatak, najprije morate da matlab pročita wav datoteku pomoću sljedećeg koda: [x, fs] = wavread ('flex4.wav'); U ovom slučaju, flex4.wav je naslov naše wav datoteke, varijabla x je podatkovna točka u datoteci, a fs se odnosi na frekvenciju uzorkovanja. Da biste izveli specgram, samo upišite sljedeći kod: specgram [x (:. 1), 256, fs]; 256 odgovara frekvenciji na kojoj se FFT izvodi pri analizi podataka. Matlab u osnovi cijepa zvučnu datoteku na komade i uzima FFT za svaki komad. 256 govori koliko bi svaki komad trebao biti velik. Pojedinosti o tome nisu važne, a 256 je sigurna vrijednost za upotrebu u većini aplikacija. Sada, ako pokrenete kôd, vidjet ćete brojku koja se pojavljuje kao što se vidi na drugoj slici. Iz ovoga je lako vidjeti da rezonantna frekvencija odgovara crvenom vrhu u donjem desnom kutu slike. Ovo je vrhunac koji najduže opstaje s obzirom na vrijeme.
Preporučeni:
Komponente za površinsko lemljenje lemljenja - Osnove lemljenja: 9 koraka (sa slikama)

Komponente za površinsko lemljenje lemljenja | Osnove lemljenja: Do sada sam u svojoj seriji Osnove lemljenja raspravljao o dovoljno osnova o lemljenju da biste mogli početi vježbati. U ovom Instructableu o čemu ću raspravljati je malo naprednije, ali to su neke od osnova za lemljenje Componenta Surface Mount Compo
Lemljenje kroz komponente rupa - Osnove lemljenja: 8 koraka (sa slikama)

Lemljenje kroz komponente rupa | Osnove lemljenja: U ovom Instructableu raspravljat ću o nekim osnovama o lemljenju komponenti kroz rupe na pločama. Pretpostavit ću da ste već provjerili prva 2 uputstva za moju seriju Osnove lemljenja. Ako niste provjerili moj In
Lemljenje žica za žice - Osnove lemljenja: 11 koraka

Lemljenje žica za žice | Osnove lemljenja: Za ovaj Instructable, raspravljat ću o uobičajenim načinima lemljenja žica na druge žice. Pretpostavit ću da ste već provjerili prva 2 uputstva za moju seriju Osnove lemljenja. Ako niste provjerili moje upute za korištenje
Upravljanje Raspberry Pi pomoću Matlaba: 5 koraka

Upravljanje Raspberry Pi pomoću Matlaba: Hej, ovaj vodič govori o kontroli vašeg malina pi bez glave pomoću matlaba. Možda ćete morati instalirati matlab na najnoviju verziju radi podrške novijem maline pi ploči
MRI otkrivanje tumora mozga pomoću Matlaba: 6 koraka
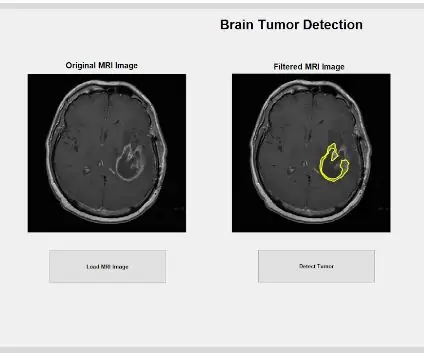
MRI otkrivanje tumora mozga pomoću Matlaba: Autor: Madhumita Kannan, Henry Nguyen, Ashley Urrutia Avila, Mei JinOvaj MATLAB kôd je program za otkrivanje točne veličine, oblika i lokacije tumora koji se nalazi u MR snimci pacijenta. Ovaj je program osmišljen tako da izvorno radi s otkrivanjem tumora
