Kako stvoriti geodetsku kupolu u stilu Temcor u Autodesk Inventoru: 8 koraka

2024 Autor: John Day | [email protected]. Zadnja promjena: 2024-01-30 09:37

Ovaj će vam vodič pokazati kako stvoriti kupolu u stilu Temcor koristeći samo malo matematike.

Većina informacija u ovom vodiču prikupljena je iz TaffGochovog obrnutog inženjeringa metode podjele stare postaje Amundsen-Scott South Pole Station, pa mu veliko hvala!

Glavna prednost Temcor kupola je njihov nizak broj jedinstvenih podupirača - aritmetički se povećava s frekvencijom, za razliku od redovne trokontaedarske geodetske mreže Duncana Stuarta (Metoda 3*), ali rezultat izgleda mnogo ugodnije.

Radi jednostavnosti, učestalost kupole koju izrađujemo je 14, pa se čimbenici akorda mogu unakrsno provjeriti s TaffGochovim Temcorovim modelom.

Inventor 2016.ipt uključen je na kraju vodiča.

*AŽURIRANJE*

Metodu 4 opisao sam kao redovitu triakontaedarsku geodetsku mrežu Duncana Stuarta, ali nije. Metodu je zapravo izumio Christopher Kitrick, koji je u svom radu iz 1985. "Geodetske kupole" opisao njezinu konstrukciju. Osim toga, u svom radu iz 1990. godine, "Jedinstven pristup geodetskim kupolama klase I, II i III", on opisuje 8 drugih metoda, od kojih je jedna metoda 3 Duncana Stuarta, druga njegova "metoda 4", i, iznenađujuće dovoljno, metoda analogna Temcorovoj, koju on naziva "Metoda aa" (Korak 7 pokazuje kako je Temcor izmijenio "Metodu aa"). U budućim instrukcijama opisat ću konstrukciju metoda navedenih u potonjem radu.

Korak 1: Korisnički parametri

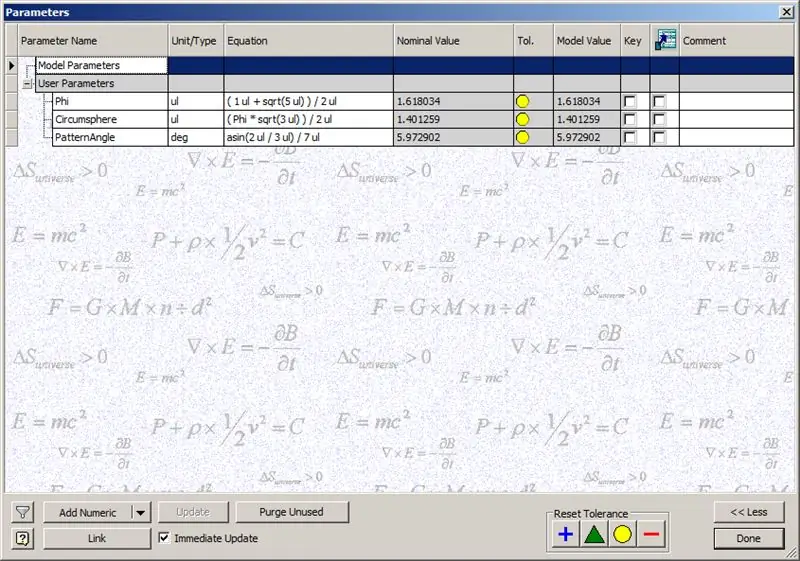
Prije nego počnemo s izgradnjom kupole, unesite prikazane parametre:

Phi - zlatni omjer. Definirano kao ((1+√5/) 2

Circumsphere - Ovo je krug dodekaedra, definiran kao ((Phi*√3)/2)

PatternAngle - Ovo je središnji kut dodekaedra. Budući da je frekvencija naše kupole 14, dijelimo ovaj središnji kut za polovicu frekvencije, u ovom slučaju 7.

Korak 2: Skiciranje zlatnog pravokutnika

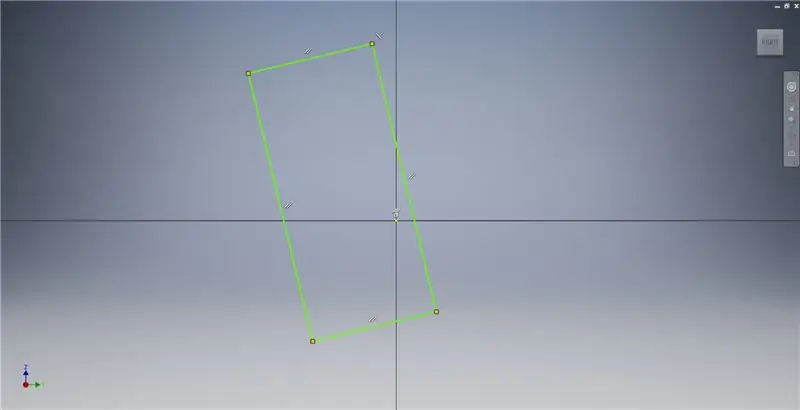
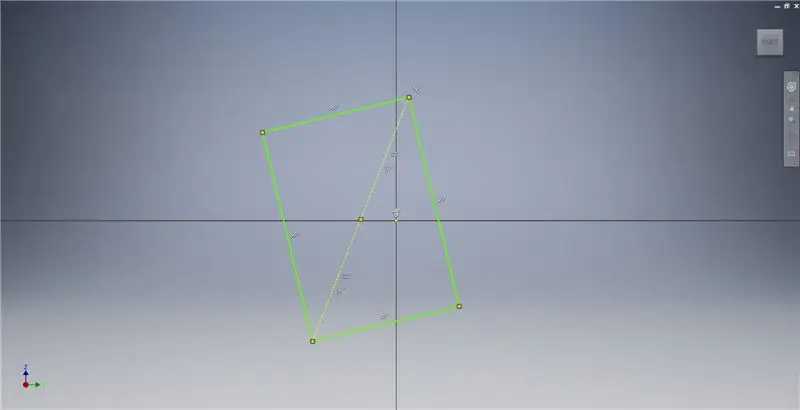
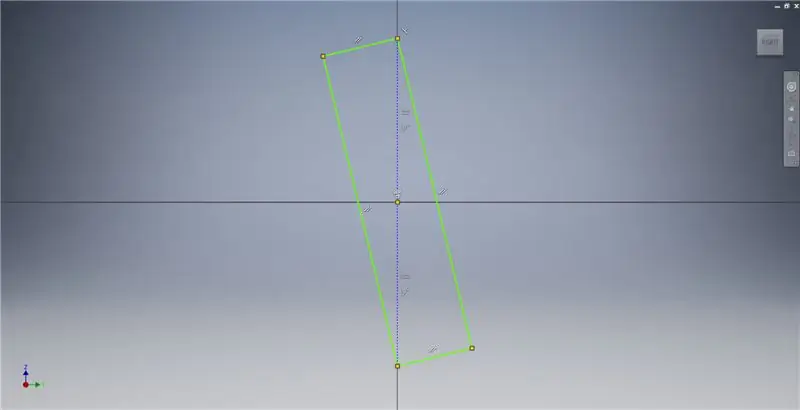
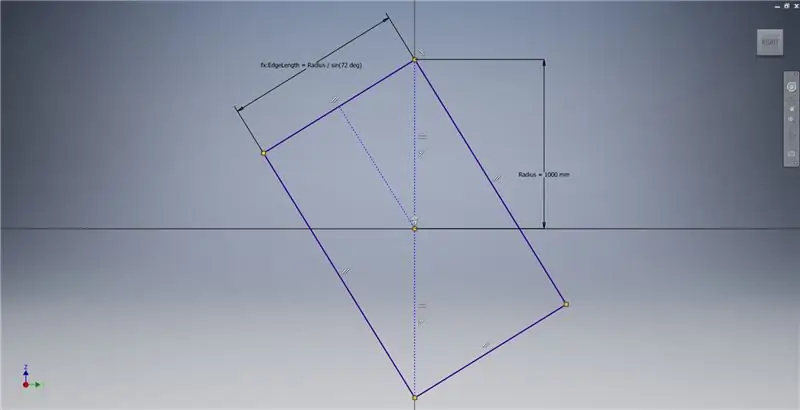
Pokrenite skicu na ravnini YZ, a zatim stvorite trokutni pravokutnik kako je prikazano, pozivajući se na bilješke sa slikama za dodatne informacije koje opisuju stvaranje zlatnog pravokutnika.

Korak 3: Stvaranje pravokutnika Golden²

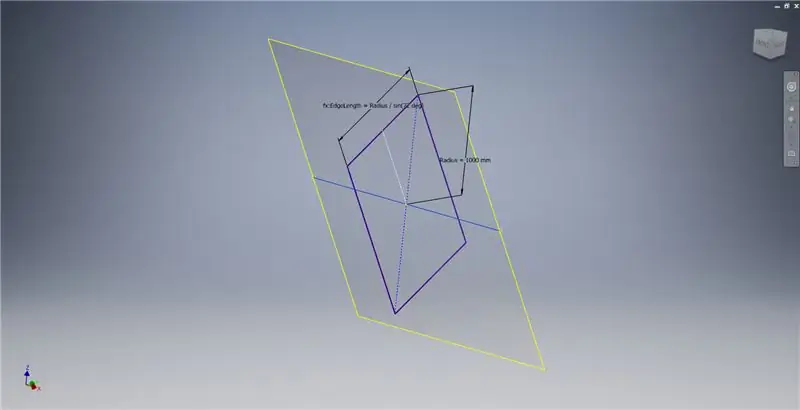
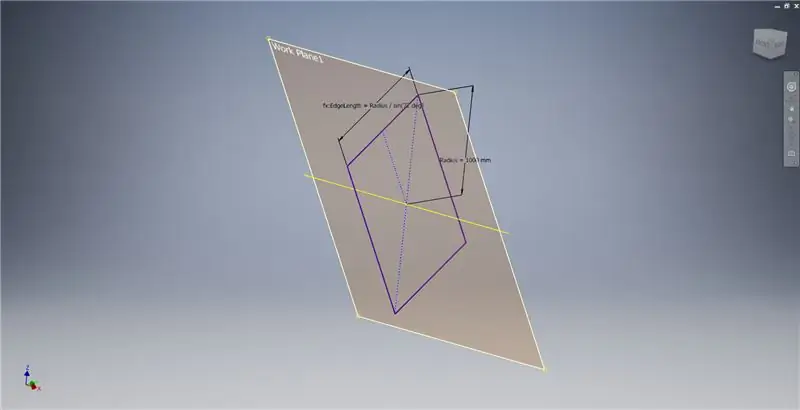
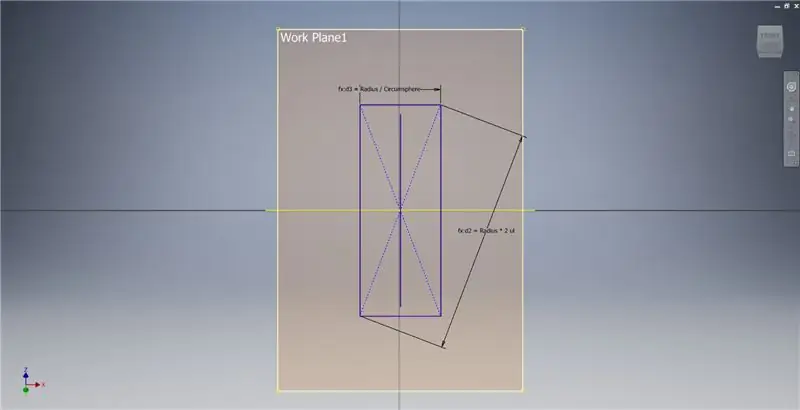
Napravite radnu ravninu pomoću osi X i crte istaknute na prvoj slici, a zatim pokrenite drugu skicu na ovoj radnoj ravnini. Konstruirajte pravokutnik središnje točke počevši od ishodišta, a zatim dimenzionirajte pravokutnik kao što je prikazano na trećoj slici.

Korak 4: Stvaranje 2v Triacon trokuta

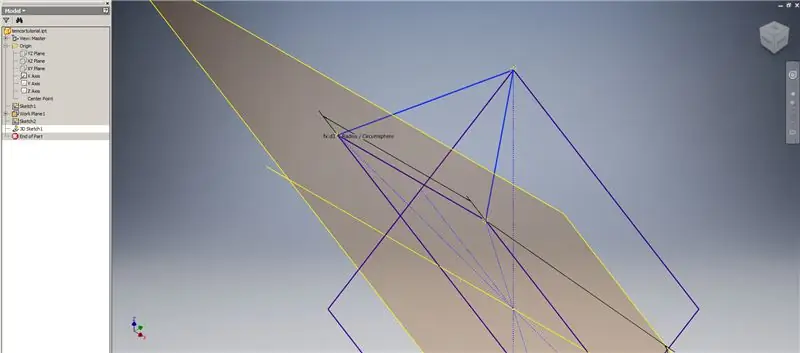
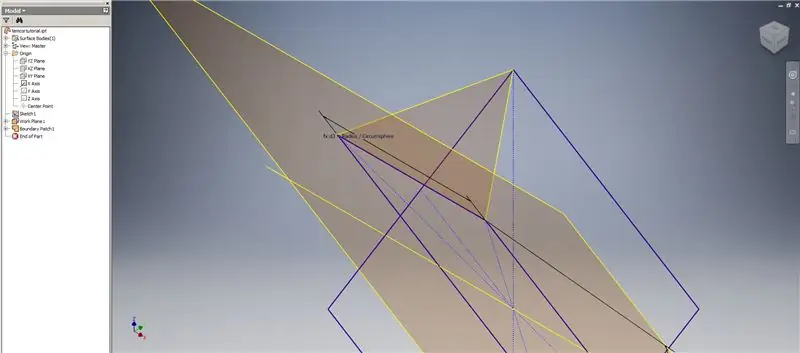
Sada kada imamo svu geometriju koja nam je potrebna, oblikujte graničnu zakrpu na drugoj slici pomoću bilo koje metode koju želite. Odlučio sam napraviti 3D skicu, ali skiciranje na drugom radnom planu jednako bi dobro funkcioniralo.

Korak 5: Stvaranje ravnina presjeka

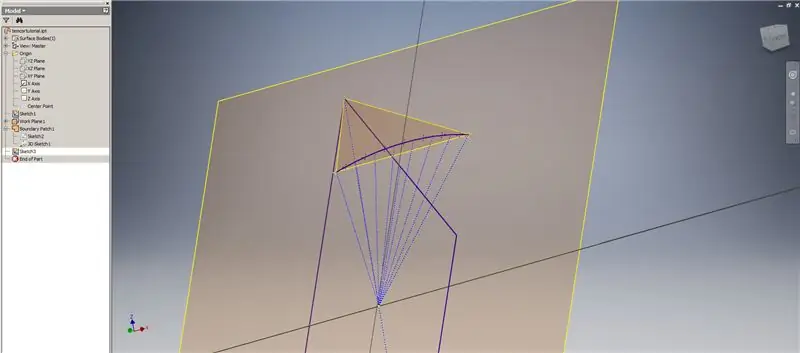
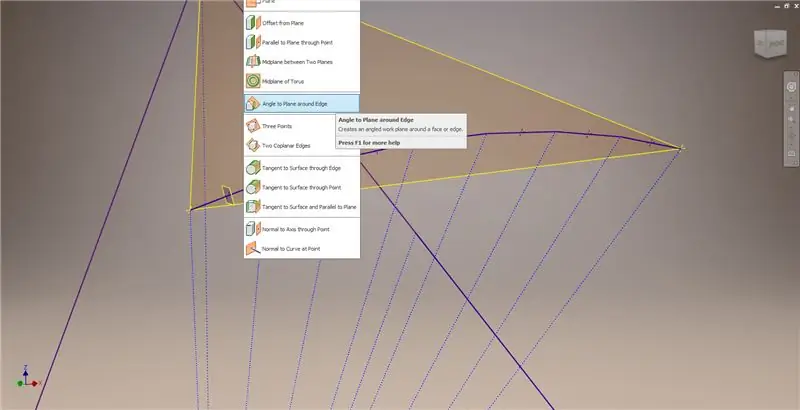
Pokrenite još jednu skicu na prvoj radnoj ravnini ("Radna ravnina 1") koju ste stvorili, projicirajte kutove pravokutnika Golden², zatim spojite ove točke i ishodište kako biste formirali središnji kut 2v trokontaedra. Podijelite ga s pola frekvencije kupole, kao da započinjete kvar Metode 2. Postavite točke na sredine akorda.

Izađite iz skice, a zatim stvorite ravninu koristeći jedan od akorda i njegovu središnju točku, kao što je prikazano na drugoj slici. Zatim stvorite drugu radnu ravninu pomoću "Kut prema ravnini oko ruba". Odaberite Radnu ravninu 1 i jednu od građevinskih linija prikazanih na sredini desno i dolje lijevo. Prihvatite zadani kut od 90 stupnjeva, inače ostatak pododjeljka ne bi izgledao dobro. Ponovite postupak pomoću ostalih akorda i konstrukcijskih linija da biste dobili rezultat na donjoj desnoj slici.

Korak 6: Stvaranje križanja presjeka i formiranje pododjela

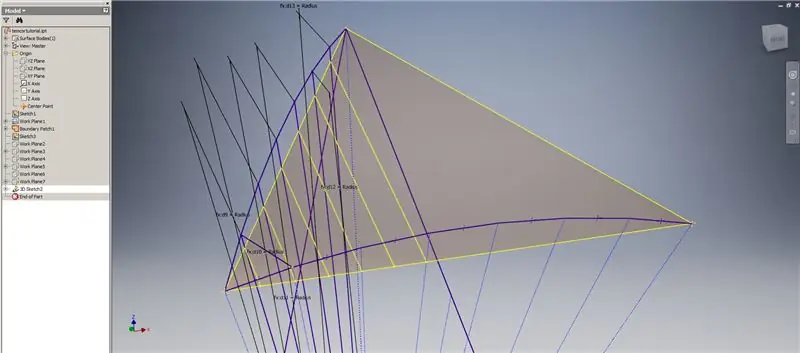
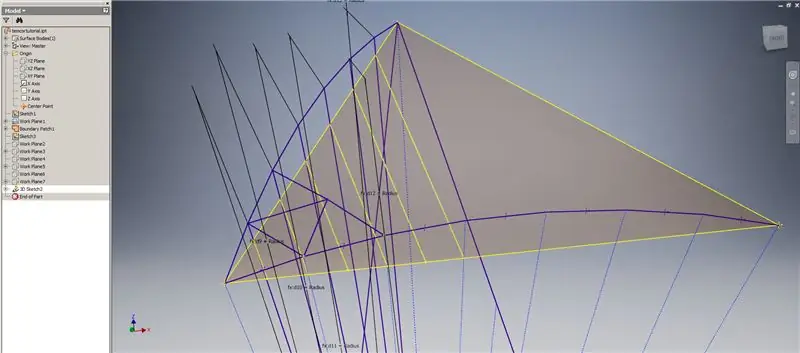
Pokrenite 3D skicu, a zatim stvorite križne križeve pomoću radnih ravnina koje ste upravo stvorili i graničnu zakrpu, tvoreći crte prikazane na gornjoj slici.

Nacrtajte linije koje se podudaraju s krajnjim točkama križnih križanja kao što je prikazano na slici 2. Neka sve budu jednake polumjeru kupole. Nacrtajte akorde koji spajaju linije koje leže na križanju presjeka. Spojite bilo koju geometriju koja izgleda dovoljno blizu da oblikujete trokut pododjela. Pogledajte sljedećih 10 slika za čije akorde želite preslikati radne ravnine sjecišta - oni to mogu objasniti bolje nego što to mogu samo riječi.

Korak 7: Dovršenje kupole

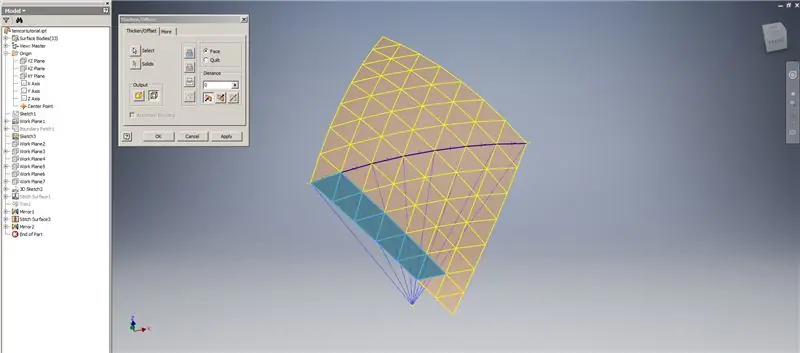
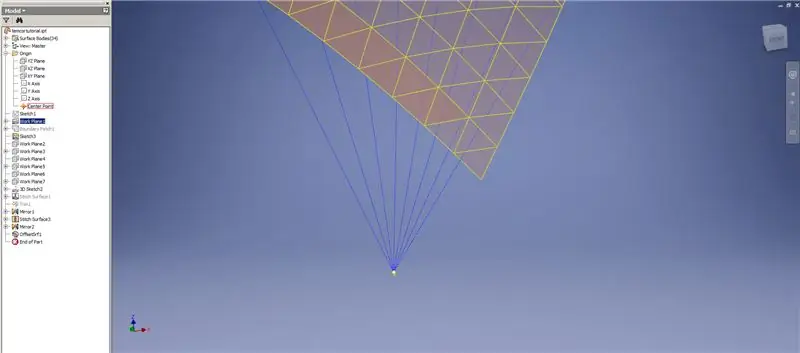
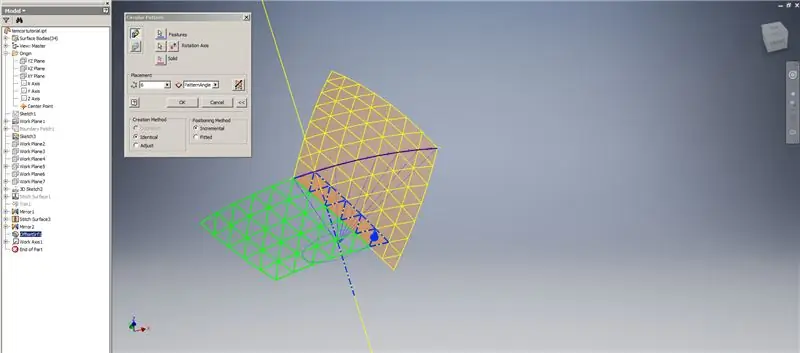
Izradite zadebljanje/pomak donjih redaka, izostavljajući posljednja dva reda trokuta. Uzorak novog OffsetSrf 6 puta, ili ((Frekvencija = 14)/2) -1. Sakrijte OffsetSrf, prošite šarene površine, a zatim zrcalite prošivenu površinu YZ ravninom. Napravite radne ravnine koje počivaju na vrhovima gornjeg trokuta, kao što je prikazano na slici 6. Obrežite zašivene i zrcalne površine pomoću ovih novih radnih ravnina, a zatim preostale površine spojite. Nacrtajte ovu zadnju površinu preko osi Z, zatim spojite ove završne površine zajedno i gotovi ste!

Korak 8: Provjeravanje akorda

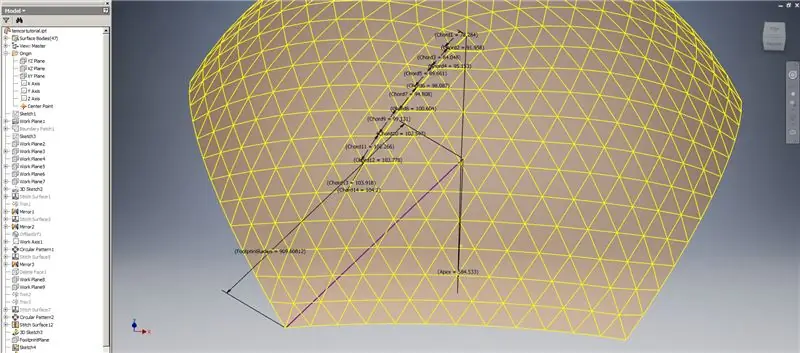
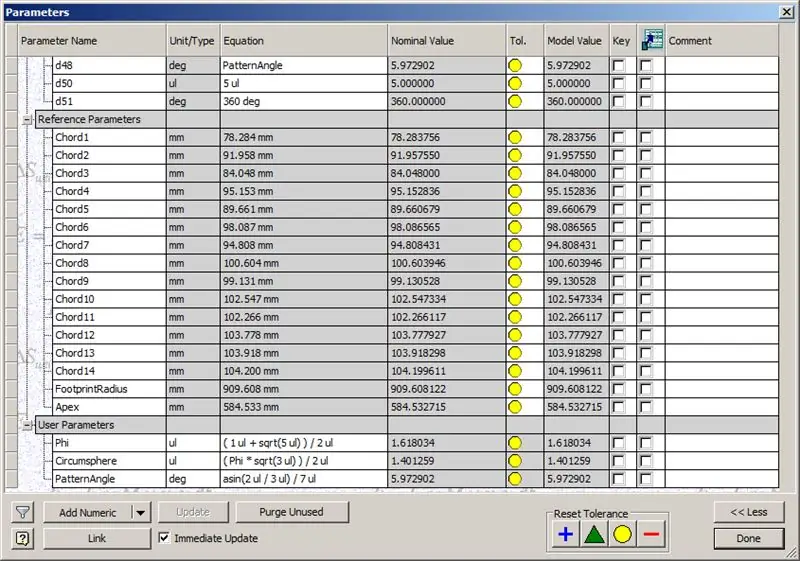
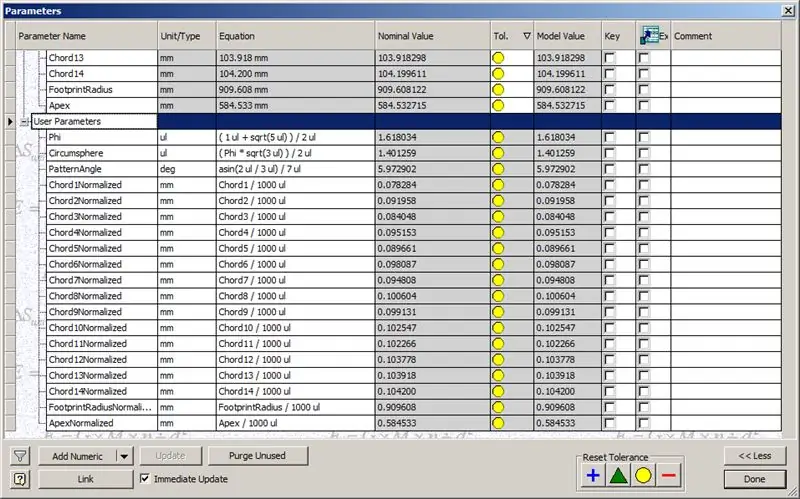
Dakle, naša kupola je gotova, ali hajde da vidimo da li se brojevi podudaraju s TaffGochovim modelom:

Ako pogledamo referentne parametre, čini se da se savršeno podudaraju!

Dijeleći duljine akorda s 1000, jasno možemo vidjeti savršenu podudarnost s faktorima akorda TaffGochovog modela, kao i faktorima polumjera i vrha stopala.